Şu an 3. Bölüm görüntüleniyor...
Örnek Soru - 1
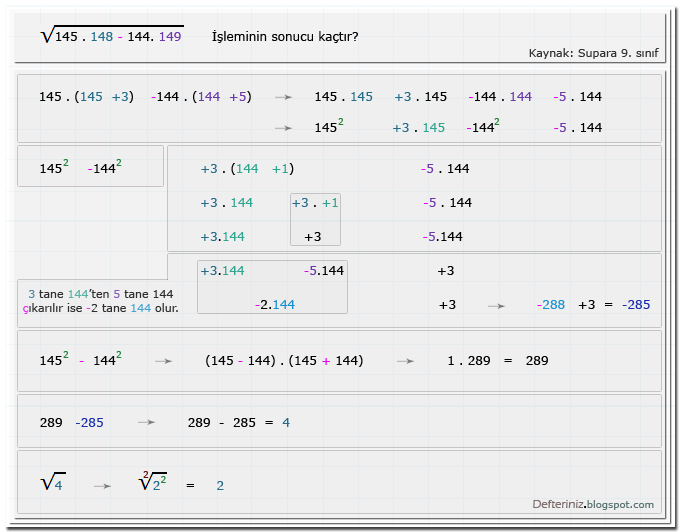
Örnek-soru-1 » Kare köklü sayıların eşleniği » kesirli merdiven işlem » çarpma ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
Not:
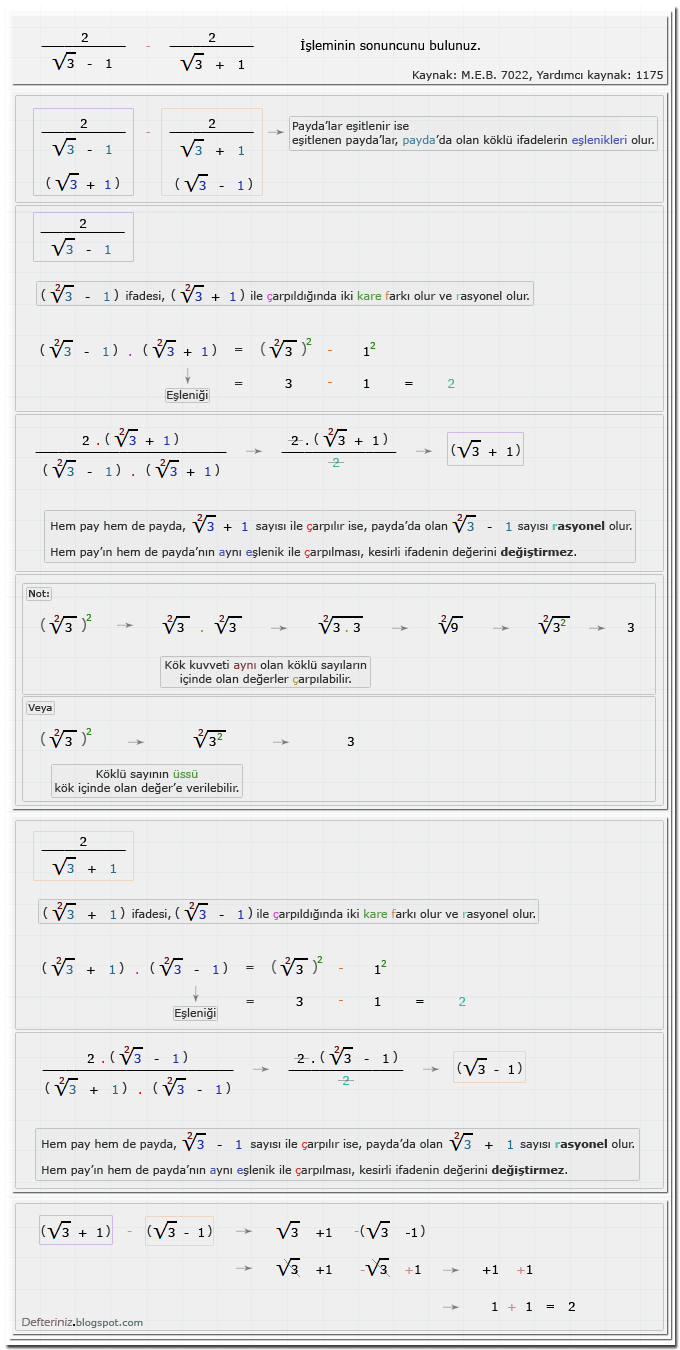
Örnek-soru-2 » Köklü kesirli ifadelerde payda'yı rasyonel yapmak » Eşlenik'ler ile payda'ları eşitlemek »iki kare farkı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 3
Örnek-soru-3 » Köklü kesirli ifadelerde payda'yı rasyonel yapmak » Eşlenik'ler ile payda'ları eşitlemek »iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek-soru-4 » Köklü kesirli ifadelerde payda'ları ayrı ayrı rasyonel yapmak » Eşlenik'ler, toplama ve çıkarma, iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 5
Örnek-soru-5 » Köklü kesirli ifadelerde payda'ları ayrı ayrı rasyonel yapmak » Eşlenik'ler, toplama ve çıkarma, iki kare farkı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 6
Örnek-soru-6 » Köklü kesirli ifade » Payda'yı rasyonel yapmak » Eşlenik, çarpma işlemi, iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 7
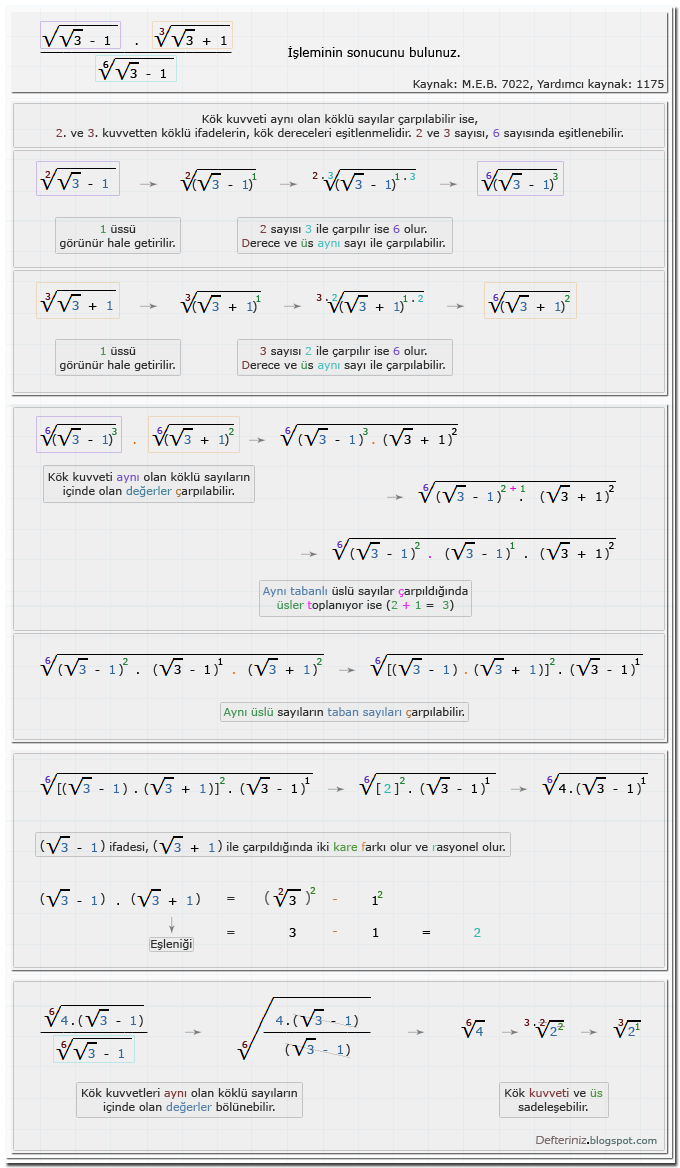
Örnek-soru-7 » Köklü kesirli ifadelerde çarpma ve bölme » Eşlenik, iki kare farkı » Kök kuvvetini eşitlemek, sadeleştirmek ve genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 8
Örnek-soru-8 » Kök kuvveti bilinmeyen olan köklü sayıların eşlenikleri (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 9
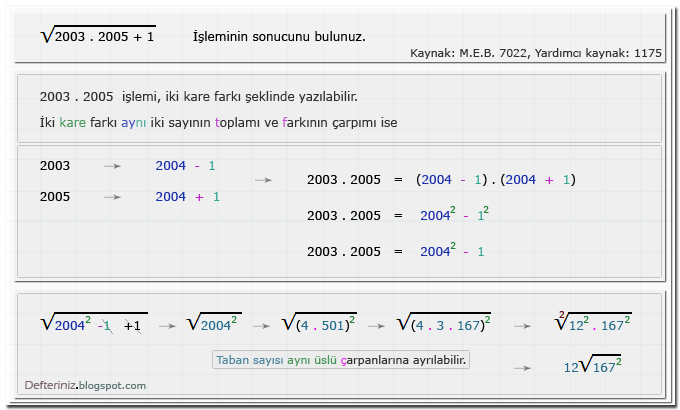
Örnek-soru-9 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 10
Örnek-soru-10 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma ve parantez işlemleri (Kaynak: Supara 9. sınıf):
Örnek Soru - 11
Örnek-soru-11 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma ve toplama işlemi ile asal çarpanlarına ayırma (Kaynak: Supara 9. sınıf):
Örnek Soru - 12
Örnek-soru-12 » Köklü kesirli ifadeler çıkarma işlemi » Payda eşitleme » İki kare farkı, toplamın ve farkın karesi (Kaynak: Supara 9. sınıf):
Örnek Soru - 13
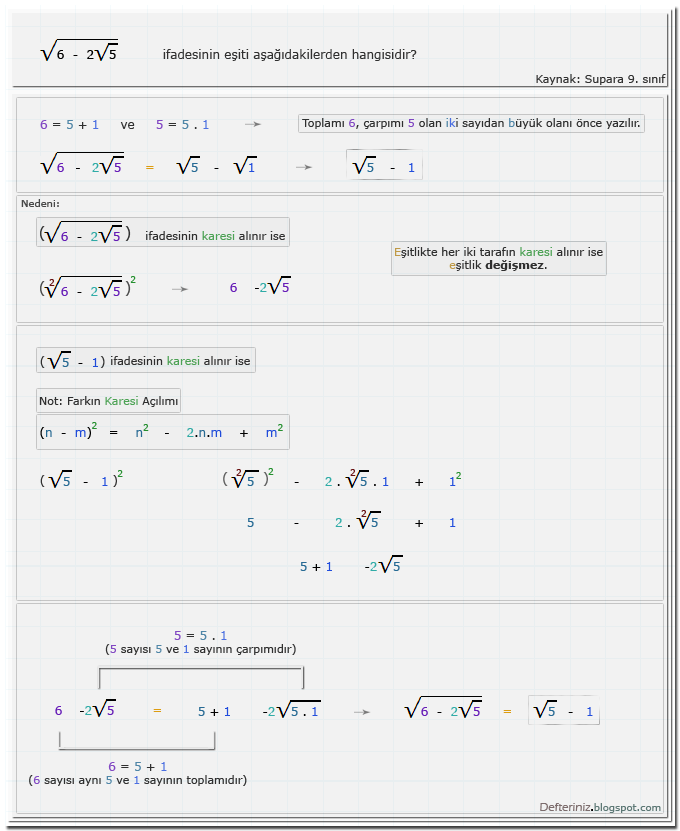
Örnek-soru-13 » Köklü ifadenin eşiti » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: Supara 9. sınıf):
Örnek Soru - 14
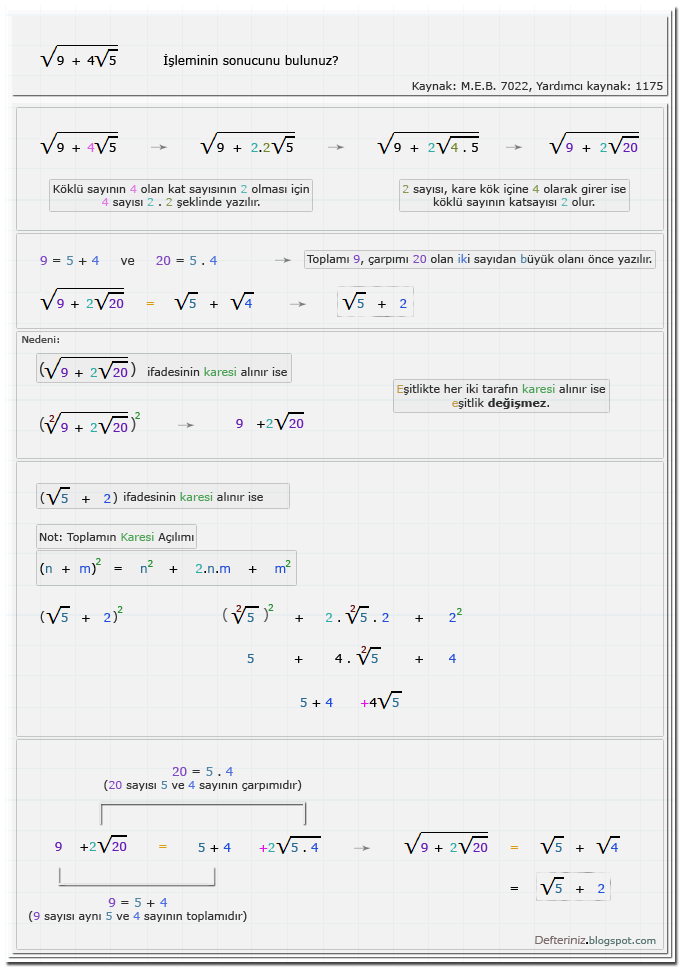
Örnek-soru-14 » Köklü ifadenin eşiti » Kök içine giren 2 sayısı ve iki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 15
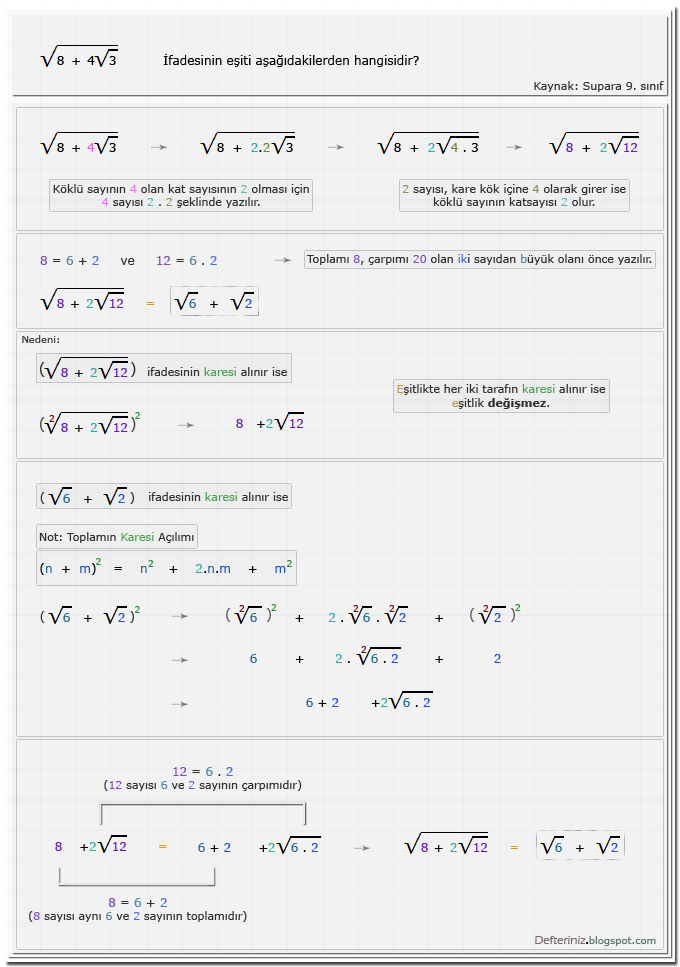
Örnek-soru-15 » Köklü ifadenin eşiti » Köklü sayının önünde 2 katsayısı » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: Supara 9. sınıf):
Örnek Soru - 16
Örnek-soru-16 » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifadelerde çıkarma işlemi » Kök içine giren ve kök dışına çıkan 2 sayısı (Kaynak: Supara 9. sınıf):
Örnek Soru - 17
Örnek-soru-17 » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifadelerde çıkarma işlemi » Kök içine giren ve kök dışına çıkan 2 sayısı (Kaynak: Supara 9. sınıf):
Örnek Soru - 18 » 1. Yol
Örnek-soru-18 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü ifadelerde çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 18 » 2. Yol
Örnek-soru-18 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü ifadelerde çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 19 » 1. Yol
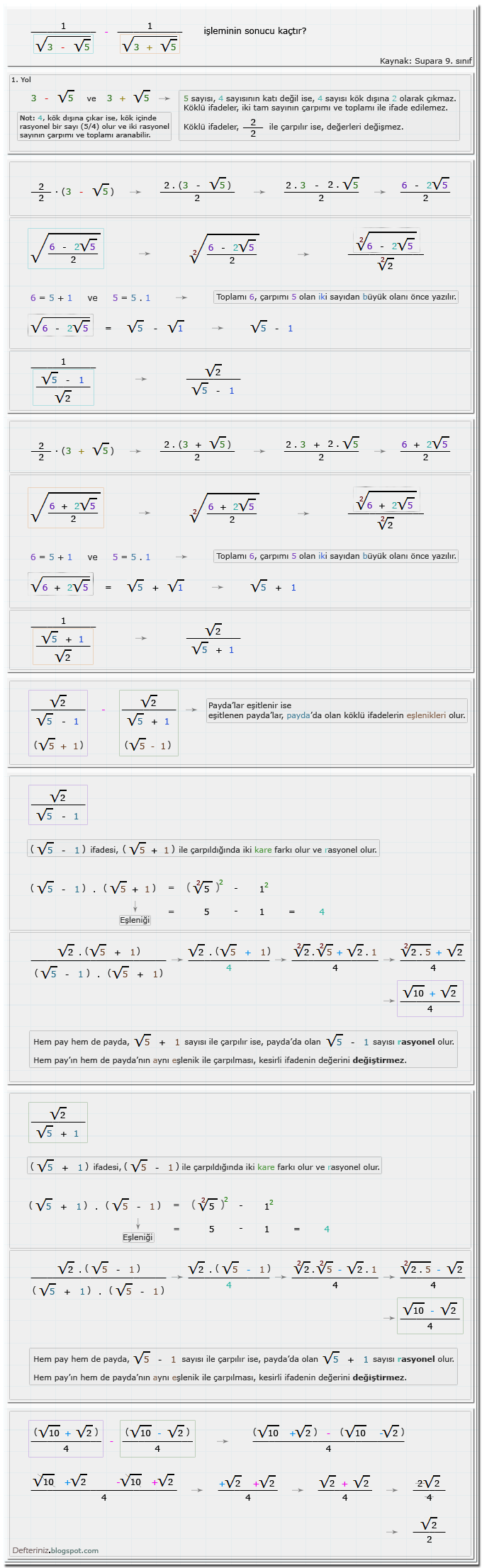
Örnek-soru-19 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadelerde çıkarma işlemi (Kaynak: Supara 9. sınıf):
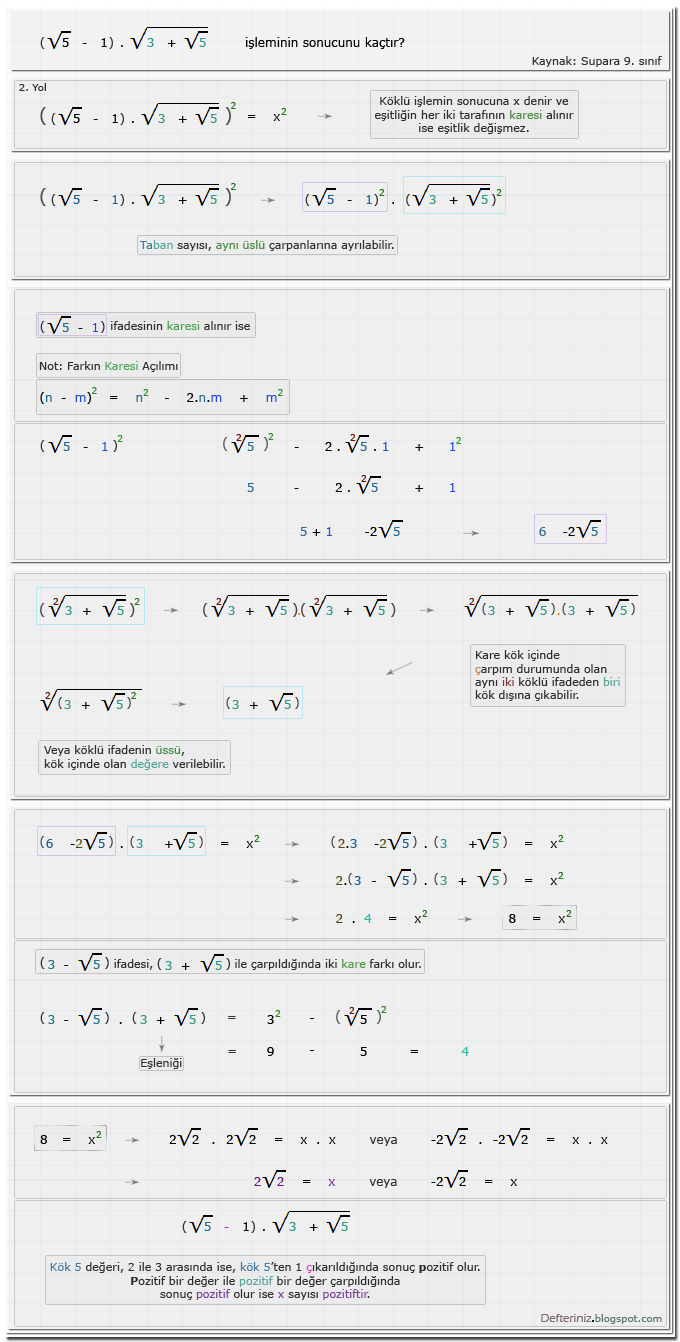
Örnek Soru - 19 » 2. Yol
Örnek-soru-19 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadelerde çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 20
Örnek-soru-20 » Köklü kesirli ifadelerde çıkarma işlemi, Payda'yı rasyonel yapmak ve eşlenikler, İki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 21 » 1. Yol
Örnek-soru-21 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadeler, İki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 21 » 2. Yol
Örnek-soru-21 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadeler, İki kare farkı, Farkın karesi (Kaynak: Supara 9. sınıf):
Örnek Soru - 22
Örnek-soru-22 » Köklü Kesirli Rasyonel İfade, İki kare farkı, Farkın karesi, Paranteze alma ve Sadeleşme işlemleri (Kaynak: Supara 9. sınıf):
Köklü Sayıların Eşlenikleri ve Payda'nın Rasyonel Yapılması
Çarpımları rasyonel olan iki irrasyonel sayıdan her biri diğerinin eşleniği olarak tanımlanır.
Köklü rasyonel ifadelerde, payda'yı kökten kurtarmak için payda'daki sayının eşleniği ile pay ve payda çarpılır.
Başka bir ifade ile, köklü sayıyı kökten kurtarıp rasyonel yapmak için, köklü sayı ile çarpılan diğer köklü sayıya, köklü sayının eşleniği denir.
Köklü rasyonel ifadelerde, payda'yı kökten kurtarmak için payda'daki sayının eşleniği ile pay ve payda çarpılır.
Başka bir ifade ile, köklü sayıyı kökten kurtarıp rasyonel yapmak için, köklü sayı ile çarpılan diğer köklü sayıya, köklü sayının eşleniği denir.
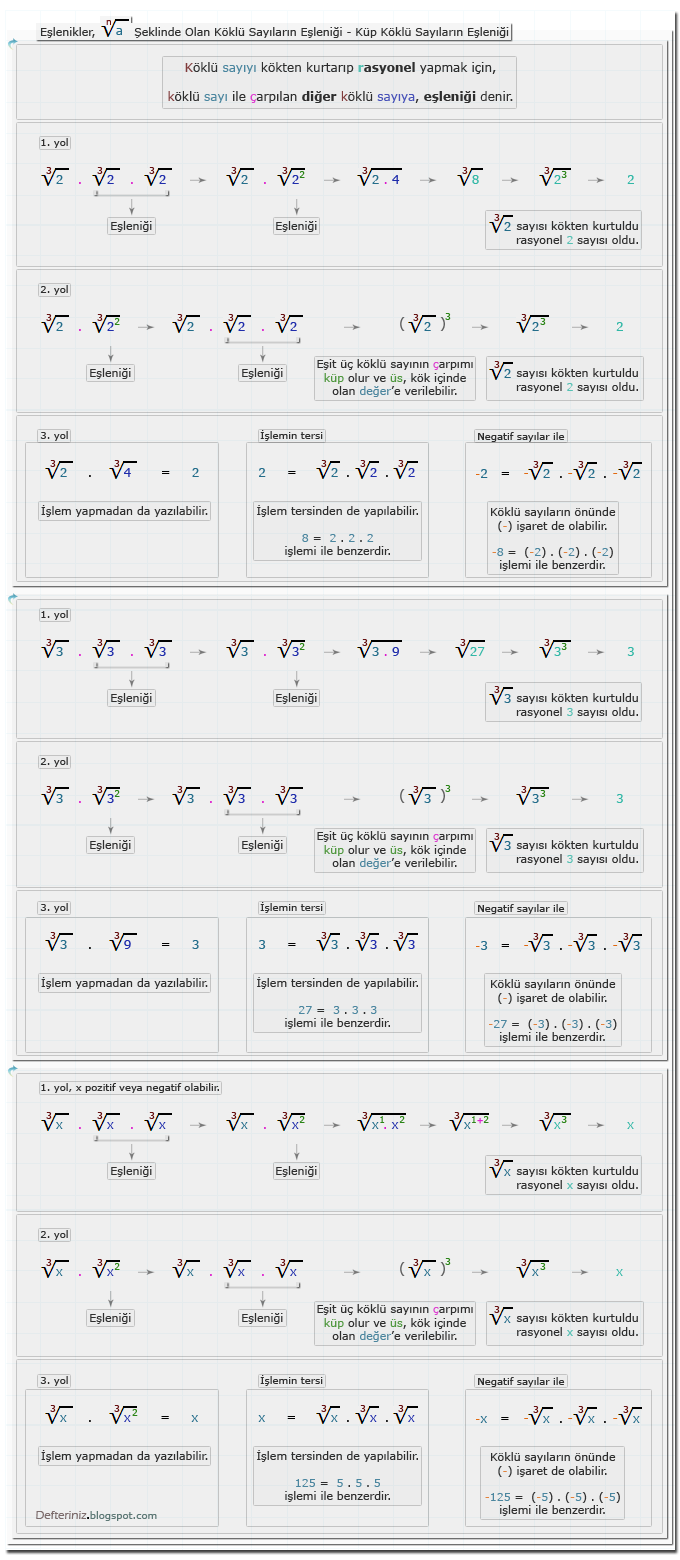
n√a Şeklinde Olan Köklü Sayıların Eşlenikleri
2. Kuvvetten Kare köklü Sayılar
Örnek-1 » 2. kuvvetten kare köklü sayıların eşleniği için örnekler:3. Kuvvetten Küp köklü Sayılar
Örnek-2 » 3. kuvvetten küp köklü sayıların eşleniği için örnekler:Payda'nın Rasyonel Yapılması, Payda'sında n√a Şeklinde Sayı Olan Köklü İfadeler
Payda'yı kökten kurtarıp rasyonel yapmak için, hem pay hem de payda, payda'da olan köklü sayının eşleniği ile çarpılır.
Payda'sında 2. Kuvvetten Kare köklü Sayı Olan Köklü İfadeler
Örnek-3 » 2. kuvvetten kare köklü sayılar » payda'nın rasyonel yapılması için örnekler:Örnek Soru - 1
Örnek-soru-1 » Kare köklü sayıların eşleniği » kesirli merdiven işlem » çarpma ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
Payda'sında 3. Kuvvetten Küp köklü Sayı Olan Köklü İfadeler
Örnek-4 » 3. kuvvetten küp köklü sayılar » payda'nın rasyonel yapılması için örnekler:Payda'sında (n√b üssü m) Şeklinde Köklü Sayı Olan Köklü İfadeler
a, b ∈ R ve n, m ∈ Z⁺ ve n ≠ 1 , b ≠ 0 ve n > m olmak üzere
Örnek-5 » (n√b üssü m) şeklinde 2. 3. 4. ve 4. kuvvetten büyük köklü sayılar » payda'nın rasyonel yapılması için örnekler:İki Kare Farkına Dönüşen √a ± √b Şeklinde Olan Köklü İfadelerin Eşlenikleri
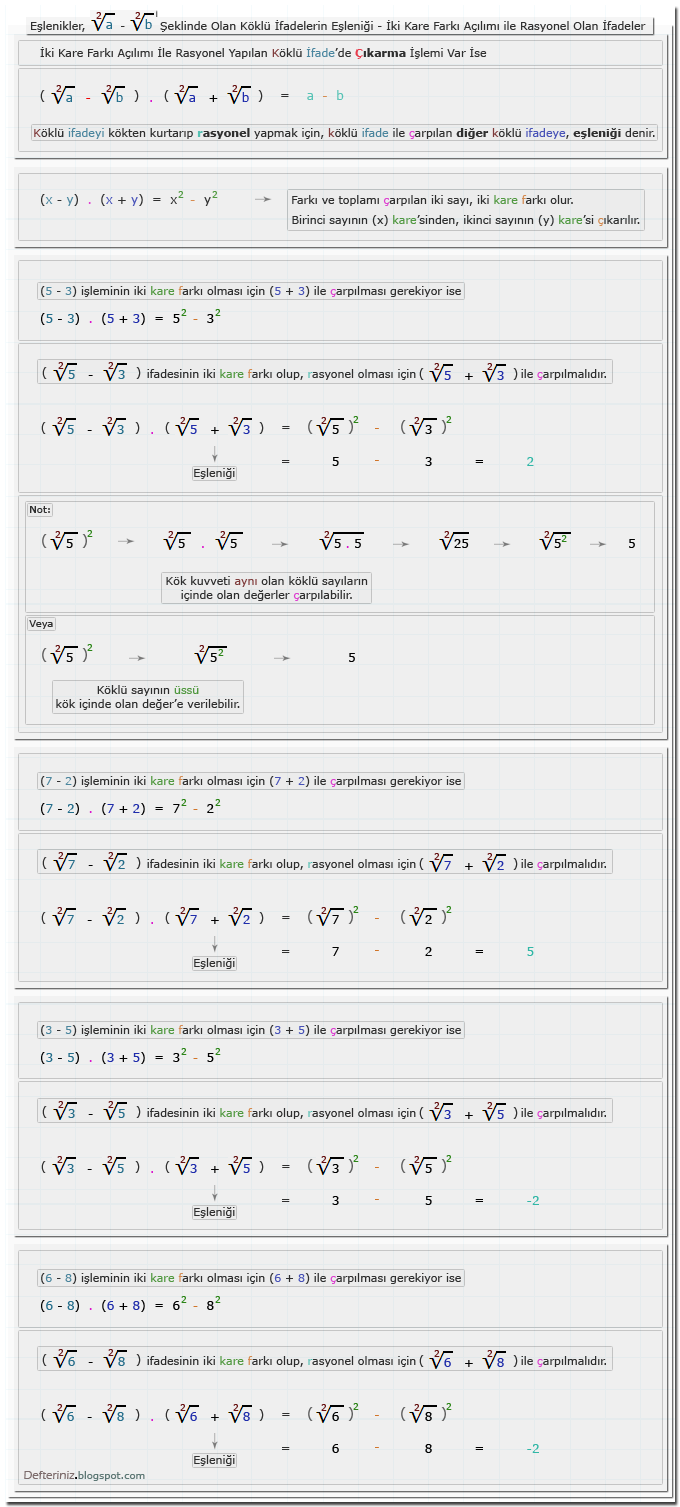
√a - √b Şeklinde Olan Köklü İfadeler
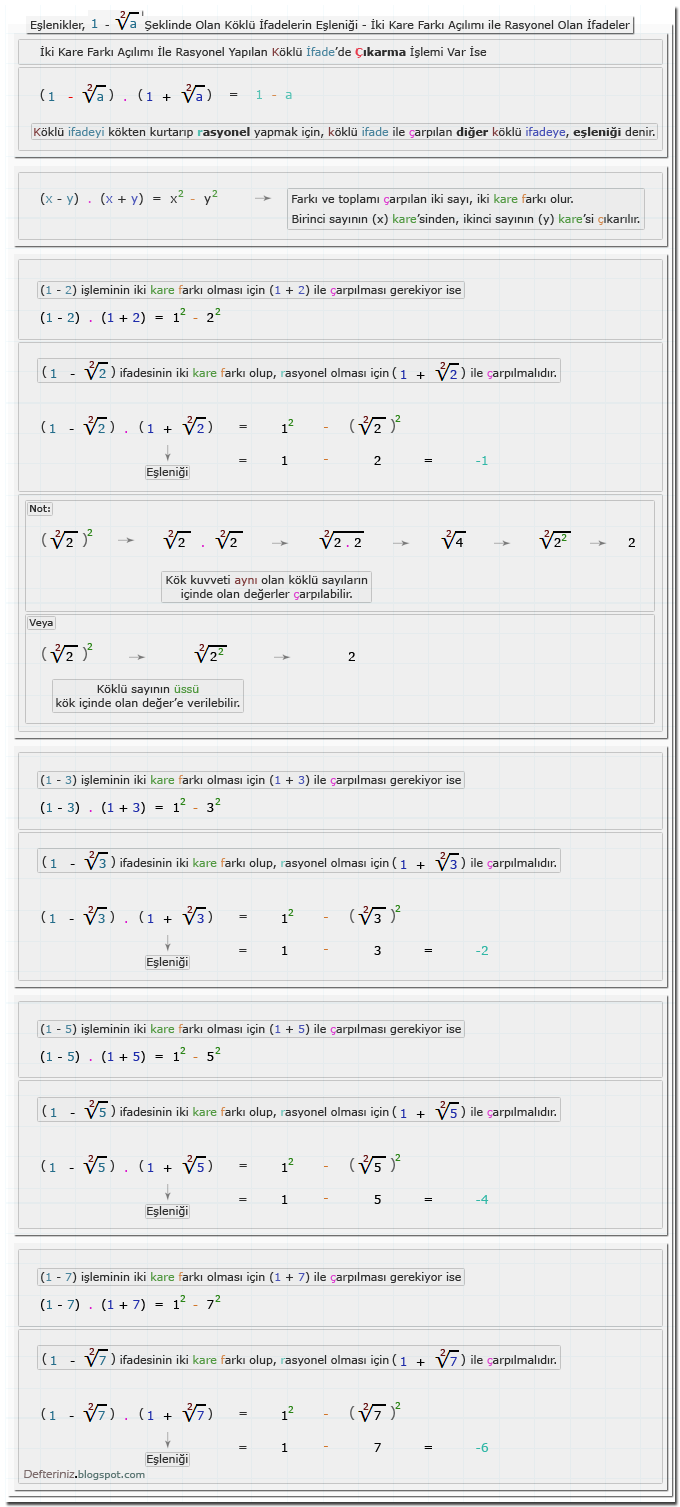
Örnek-6 » √a - √b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:1 - √a Şeklinde Olan Köklü İfadeler
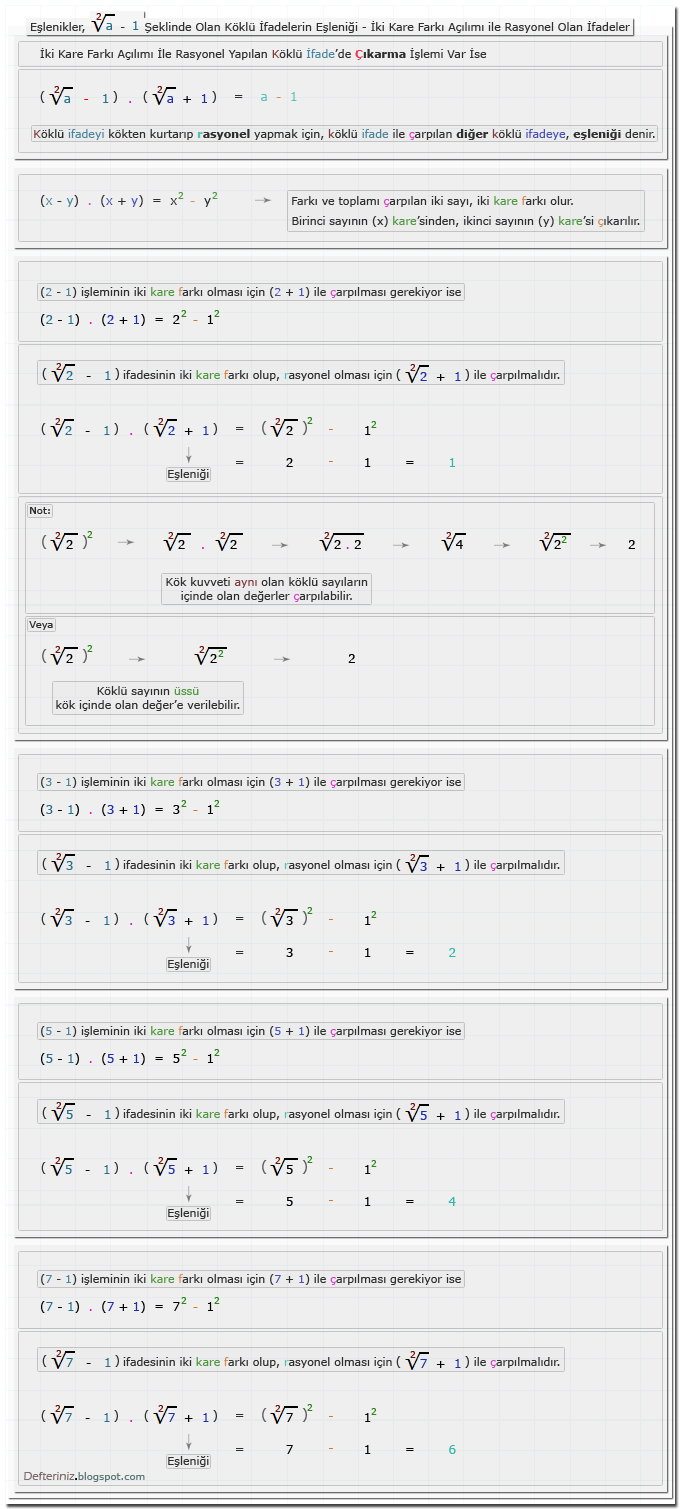
Örnek-7 » 1 - √a şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:√a - 1 Şeklinde Olan Köklü İfadeler
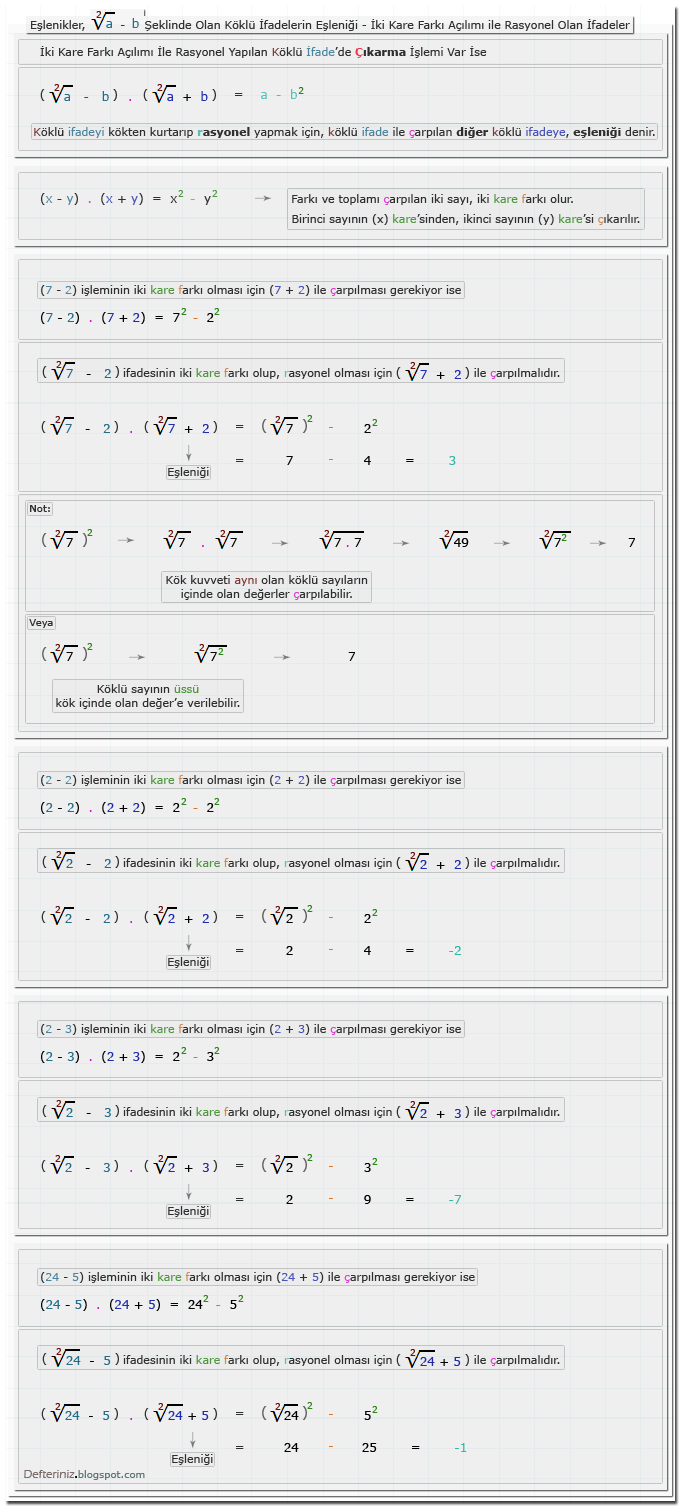
Örnek-8 » √a - 1 şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:a - √b Şeklinde Olan Köklü İfadeler
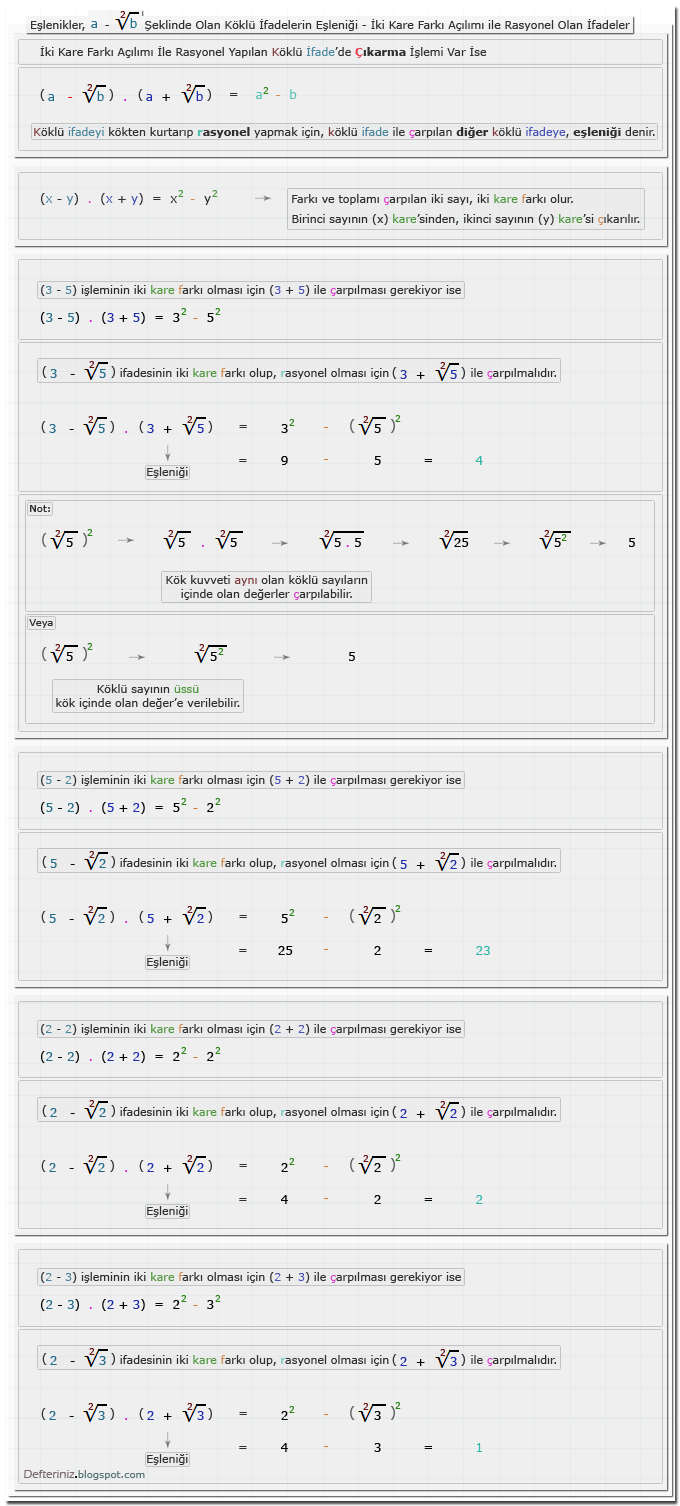
Örnek-9 » a - √b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:√a - b Şeklinde Olan Köklü İfadeler
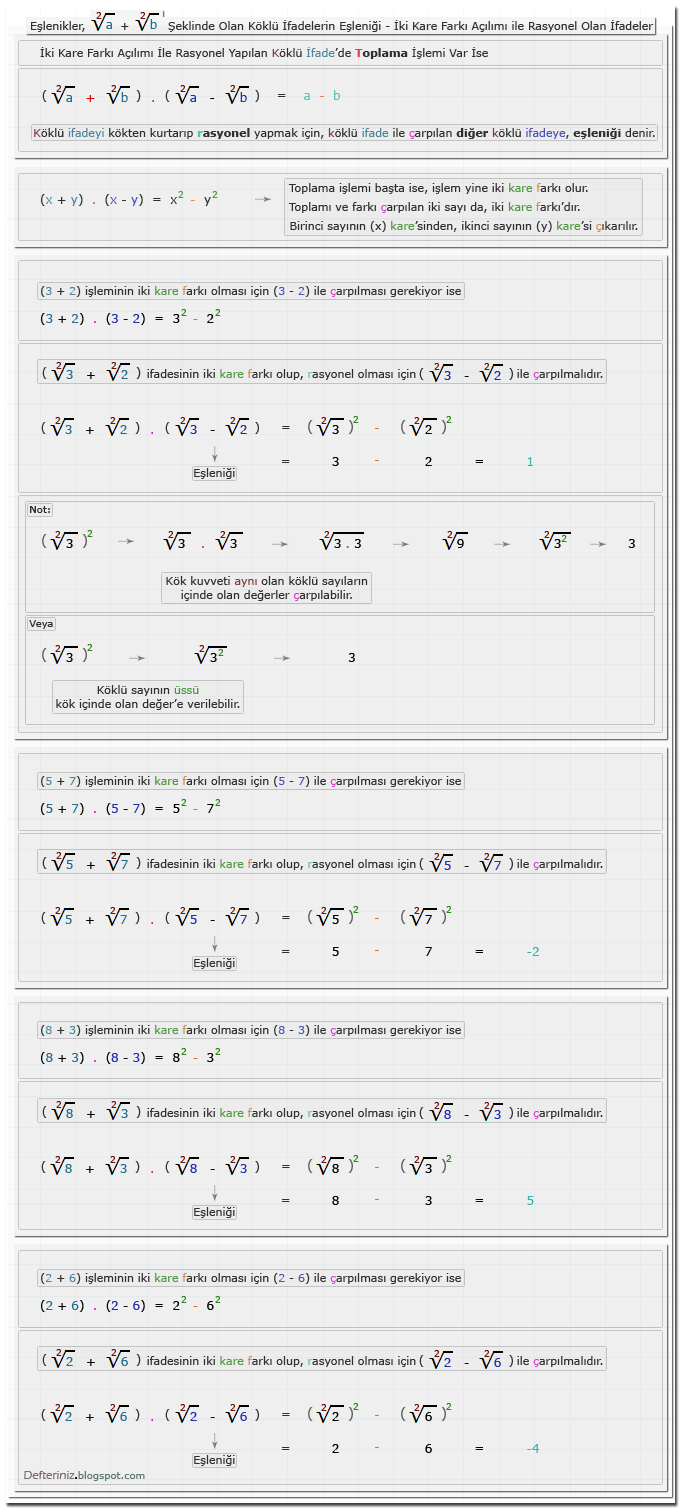
Örnek-10 » √a - b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:√a + √b Şeklinde Olan Köklü İfadeler
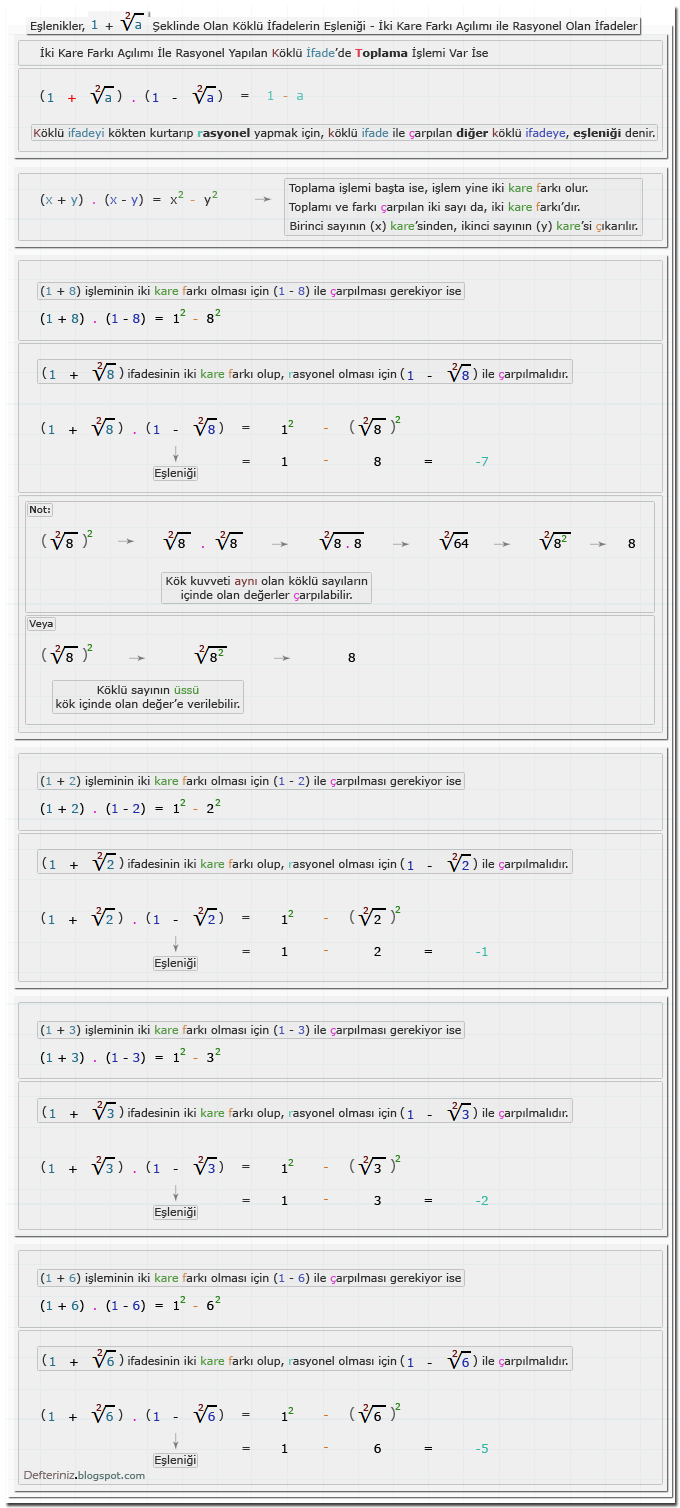
Örnek-11 » √a + √b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:1 + √a Şeklinde Olan Köklü İfadeler
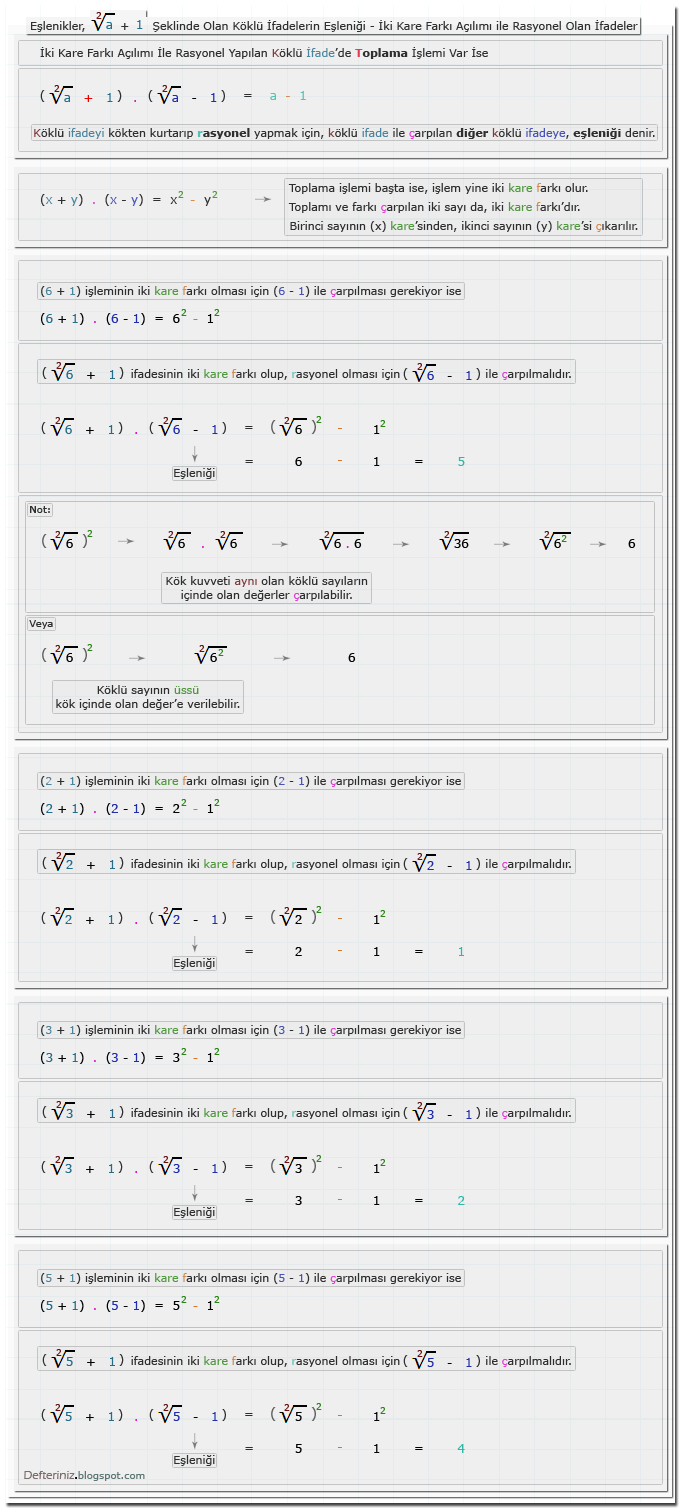
Örnek-12 » 1 + √a şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:√a + 1 Şeklinde Olan Köklü İfadeler
Örnek-13 » √a + 1 şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:a + √b Şeklinde Olan Köklü İfadeler
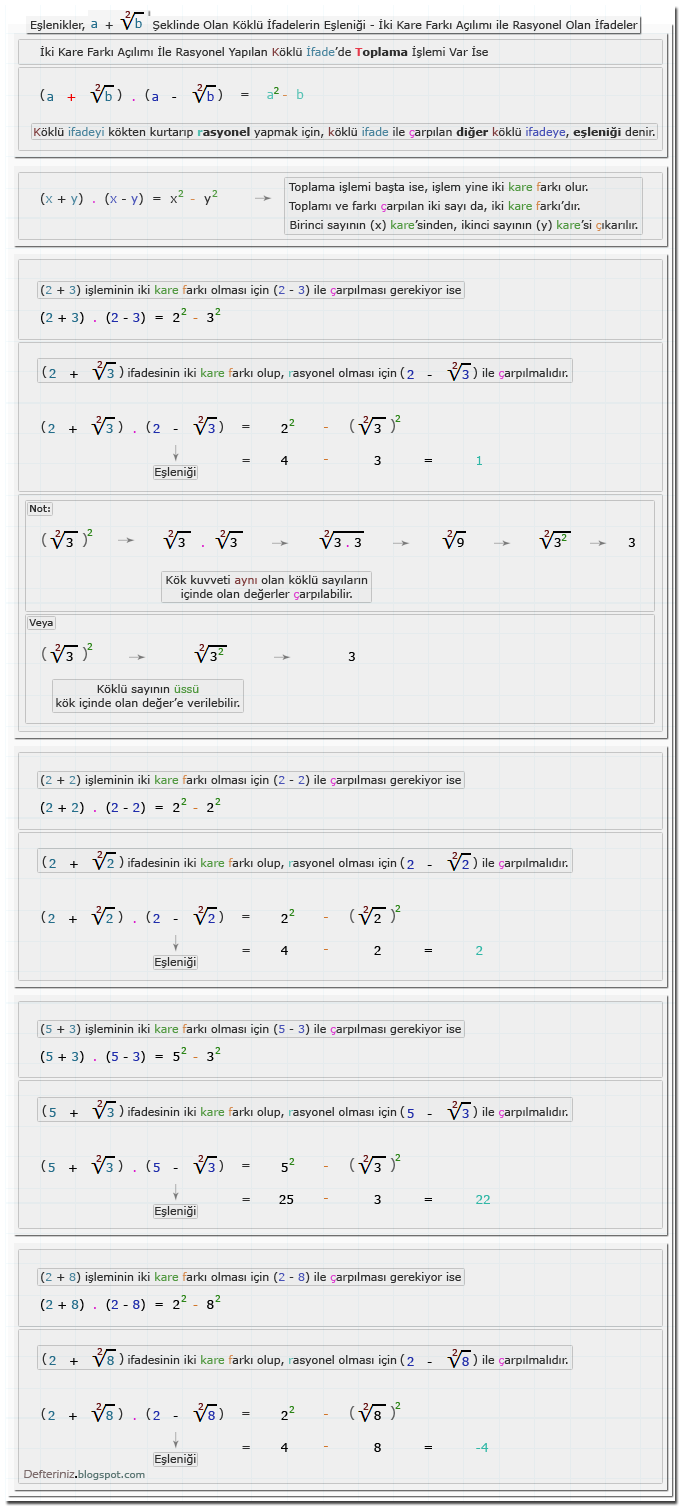
Örnek-14 » a + √b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:√a + b Şeklinde Olan Köklü İfadeler
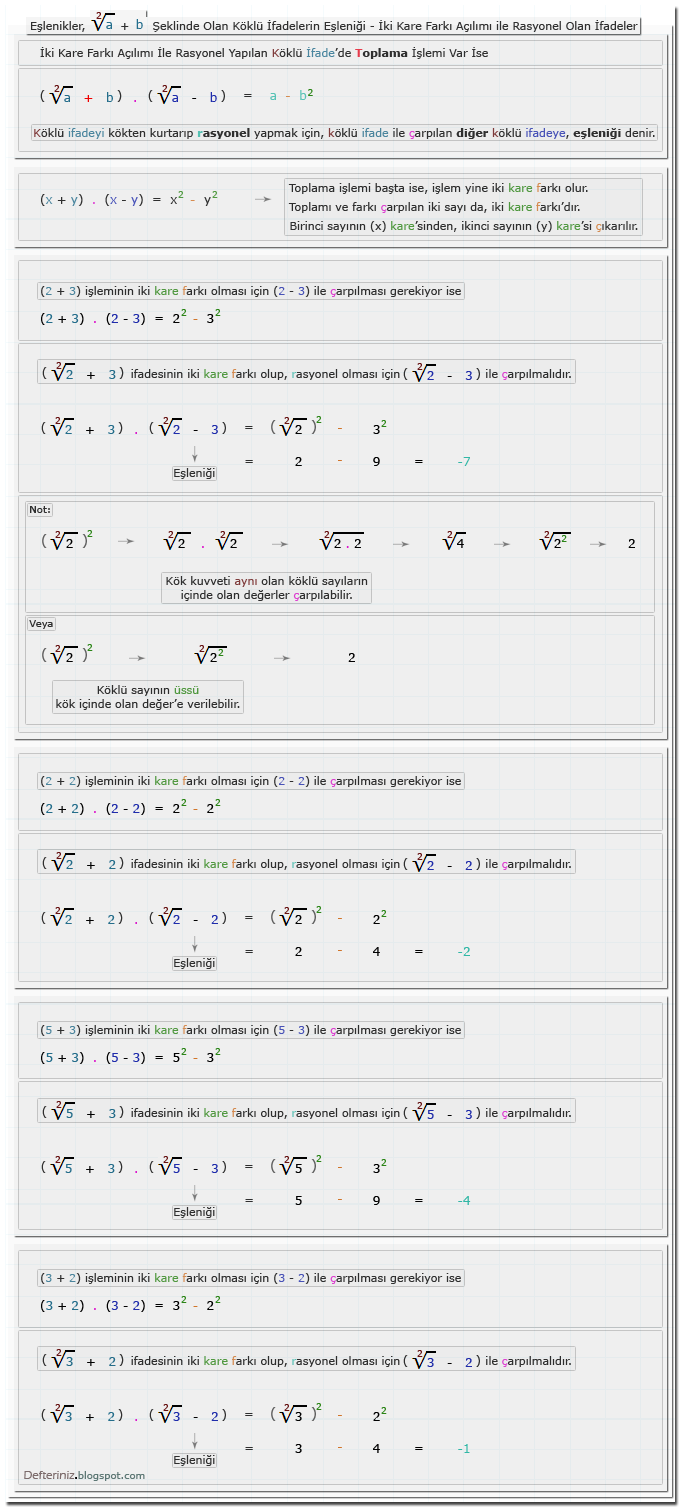
Örnek-15 » √a + b şeklinde olan köklü ifadeleri iki kare farkına dönüştüren eşleniği ile çarpmak:Payda'nın Rasyonel Yapılması, İki Kare Farkına Dönüşen √a ± √b Şeklinde Olan Köklü İfadeler
√a - √b ve √a + √b Şeklinde Olan Köklü İfadeler
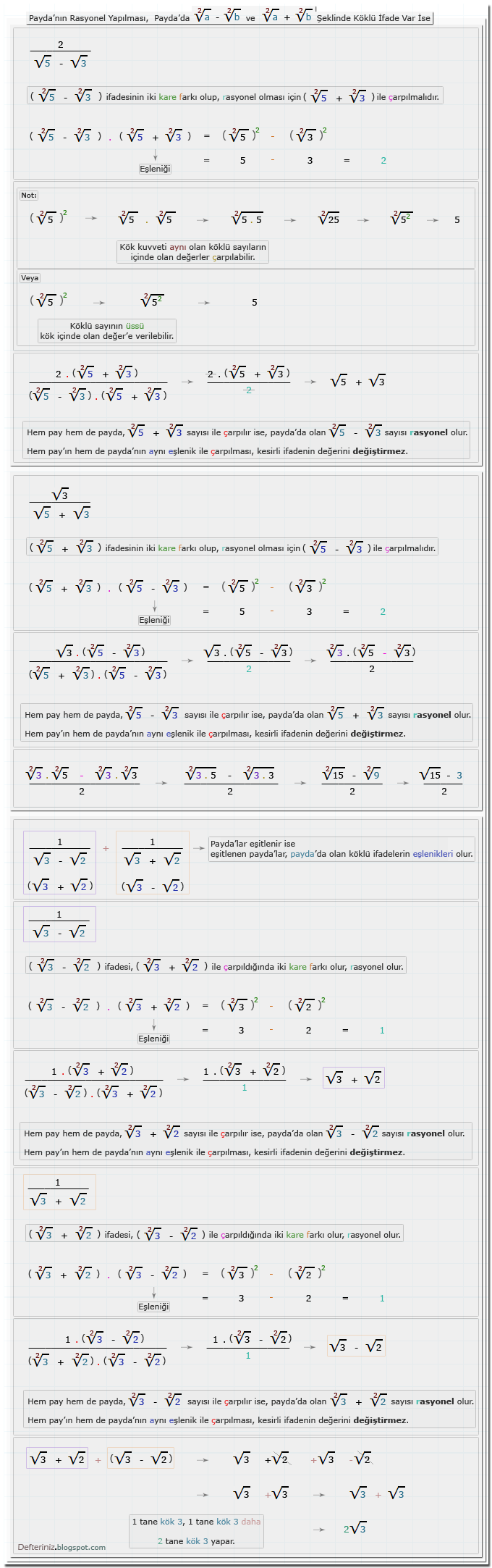
Örnek-16 » Payda'nın rasyonel yapılması » Payda'da √a - √b ve √a + √b şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar:1 - √a ve 1 + √a Şeklinde Olan Köklü İfadeler
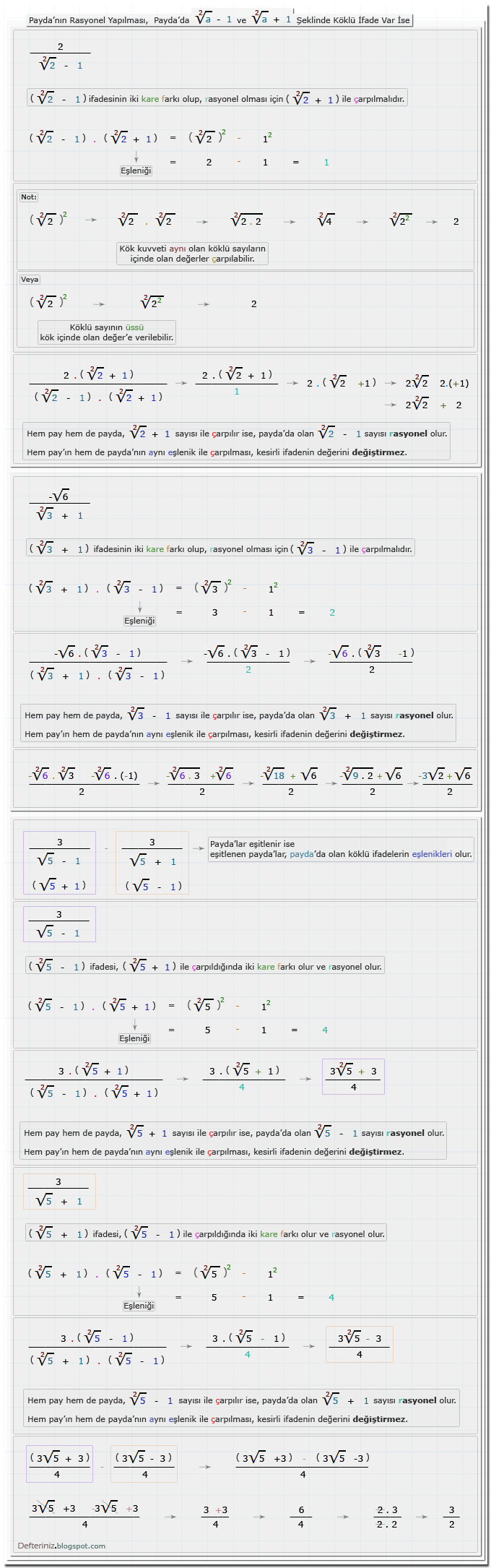
Örnek-17 » Payda'nın rasyonel yapılması » Payda'da 1 - √a ve 1 + √a şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar:√a - 1 ve √a + 1 Şeklinde Olan Köklü İfadeler
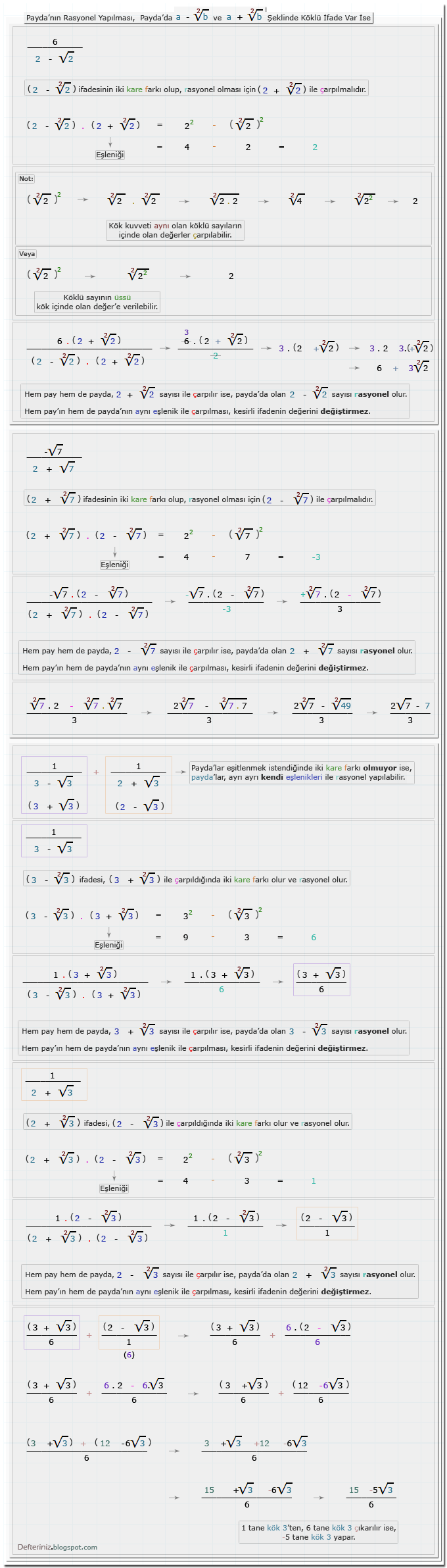
Örnek-18 » Payda'nın rasyonel yapılması » Payda'da √a - 1 ve √a + 1 şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar:a - √b ve a + √b Şeklinde Olan Köklü İfadeler
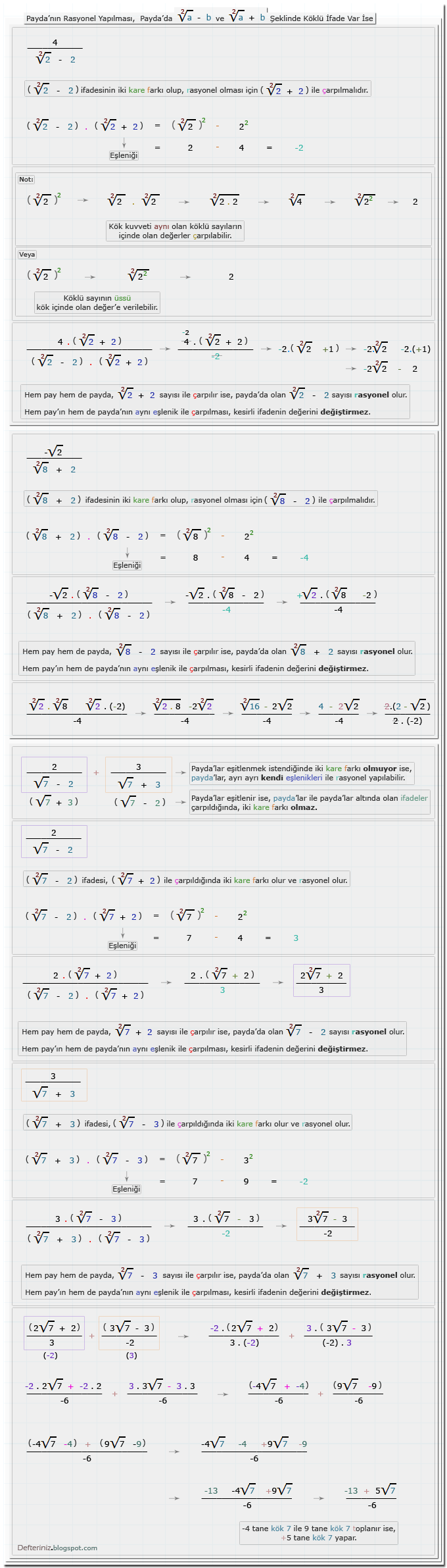
Örnek-19 » Payda'nın rasyonel yapılması » Payda'da a - √b ve a + √b şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar:√a - b ve √a + b Şeklinde Olan Köklü İfadeler
Örnek-20 » Payda'nın rasyonel yapılması » Payda'da √a - b ve √a + b şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar:(a - √b) ve (-a - √b) Şeklinde Olan Köklü İfadeler
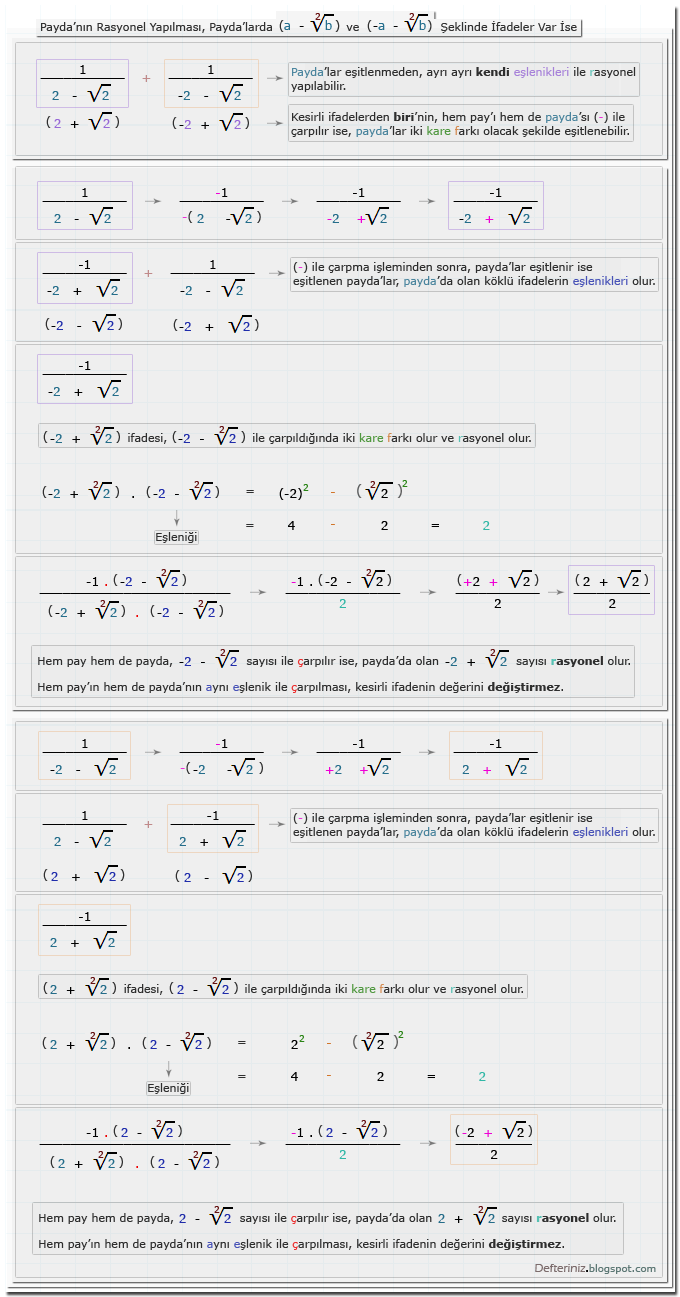
Örnek-21 » Payda'nın rasyonel yapılması » Payda'da (a - √b) ve (-a - √b) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:(a + √b) ve (-a + √b) Şeklinde Olan Köklü İfadeler
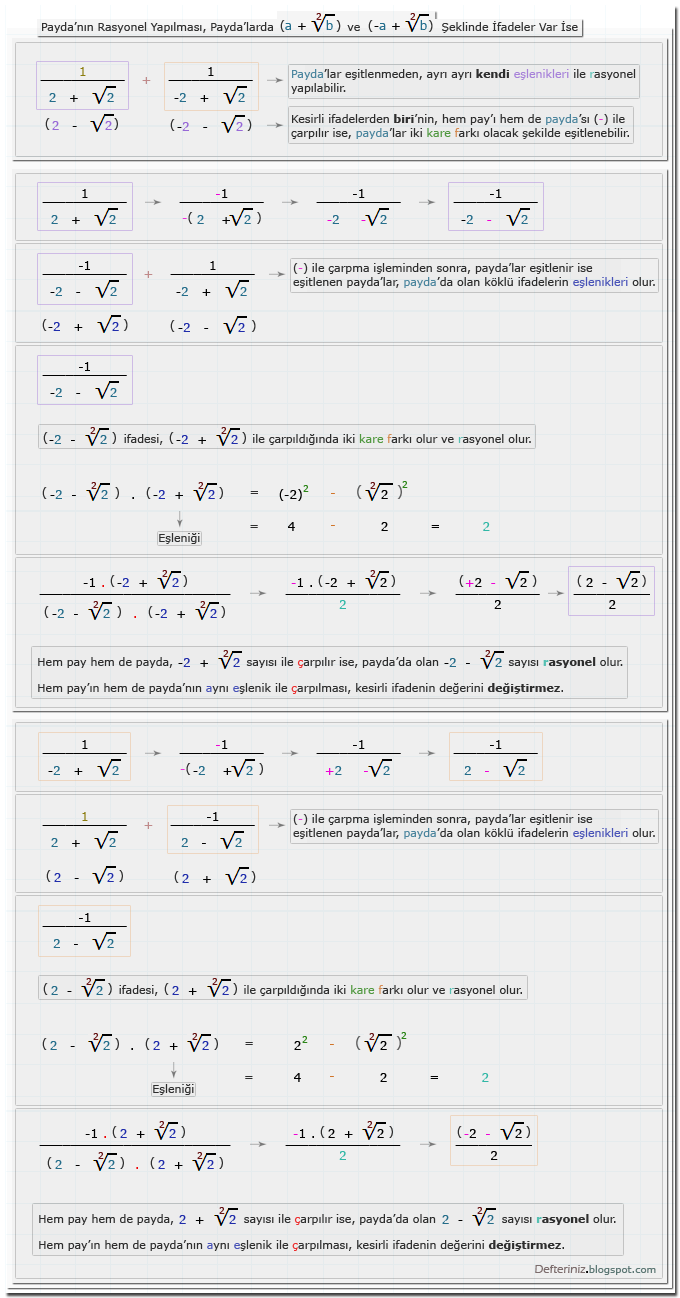
Örnek-22 » Payda'nın rasyonel yapılması » Payda'da (a + √b) ve (-a + √b) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:(√a - b) ve (-√a - b) Şeklinde Olan Köklü İfadeler
Örnek-23 » Payda'nın rasyonel yapılması » Payda'da (√a - b) ve (-√a - b) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:(√a + b) ve (-√a + b) Şeklinde Olan Köklü İfadeler
Örnek-24 » Payda'nın rasyonel yapılması » Payda'da (√a + b) ve (-√a + b) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:(√a + b) ve (b - √a) Şeklinde Olan Köklü İfadeler
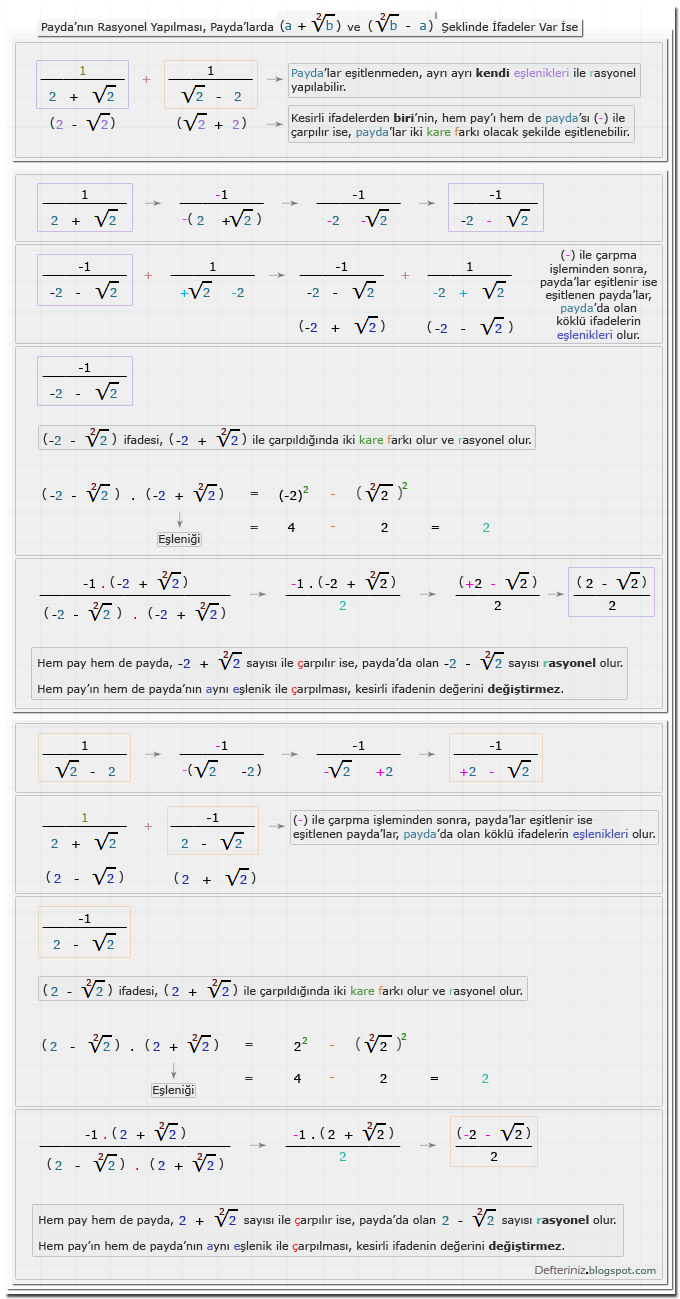
Örnek-25 » Payda'nın rasyonel yapılması » Payda'da (√a + b) ve (b - √a) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:(a + √b) ve (√b - a) Şeklinde Olan Köklü İfadeler
Örnek-26 » Payda'nın rasyonel yapılması » Payda'da (a + √b) ve (√b - a) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Payda'lardan biri (-) ile çarpılıyor ise:Toplama İşleminin Değişme Özelliği ile (√a + b) ve (b - √a) Şeklinde Olan Köklü İfadeler
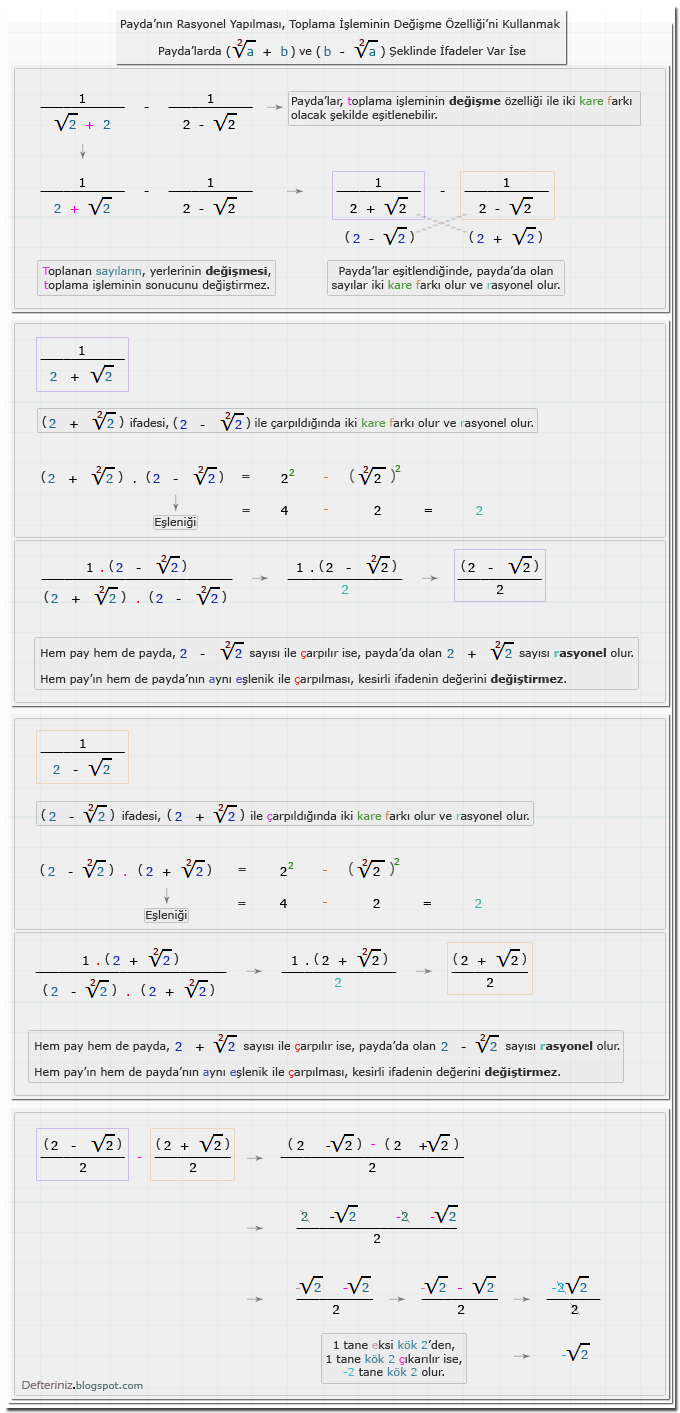
Örnek-27 » Payda'nın rasyonel yapılması » Payda'da (√a + b) ve (b - √a) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Toplama işleminin değişme özelliği:Toplama İşleminin Değişme Özelliği ile (a + √b) ve (√b - a) Şeklinde Olan Köklü İfadeler
Örnek-28 » Payda'nın rasyonel yapılması » Payda'da (a + √b) ve (√b - a) şeklinde köklü ifade var ise » Eşleniği ile iki kare farkına dönüştürülen payda'lar » Toplama işleminin değişme özelliği:Not:
Tüm kesirli işlem türleri ezberlenmek zorunda değildir.
İşlemlerde; toplama işleminin değişme özelliği veya pay'ı ve payda'yı (-) ile çarpmak işlemleri, kesirli işleme göre değerlendirilmelidir.
Pay'ı ve payda'yı (-) ile çarpmak işlemi yerine, toplama işleminin değişme özelliğini kullanmak da mümkündür.
Örnek Soru - 2İşlemlerde; toplama işleminin değişme özelliği veya pay'ı ve payda'yı (-) ile çarpmak işlemleri, kesirli işleme göre değerlendirilmelidir.
Pay'ı ve payda'yı (-) ile çarpmak işlemi yerine, toplama işleminin değişme özelliğini kullanmak da mümkündür.
Örnek-soru-2 » Köklü kesirli ifadelerde payda'yı rasyonel yapmak » Eşlenik'ler ile payda'ları eşitlemek »iki kare farkı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 3
Örnek-soru-3 » Köklü kesirli ifadelerde payda'yı rasyonel yapmak » Eşlenik'ler ile payda'ları eşitlemek »iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek-soru-4 » Köklü kesirli ifadelerde payda'ları ayrı ayrı rasyonel yapmak » Eşlenik'ler, toplama ve çıkarma, iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 5
Örnek-soru-5 » Köklü kesirli ifadelerde payda'ları ayrı ayrı rasyonel yapmak » Eşlenik'ler, toplama ve çıkarma, iki kare farkı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 6
Örnek-soru-6 » Köklü kesirli ifade » Payda'yı rasyonel yapmak » Eşlenik, çarpma işlemi, iki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 7
Örnek-soru-7 » Köklü kesirli ifadelerde çarpma ve bölme » Eşlenik, iki kare farkı » Kök kuvvetini eşitlemek, sadeleştirmek ve genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 8
Örnek-soru-8 » Kök kuvveti bilinmeyen olan köklü sayıların eşlenikleri (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 9
Örnek-soru-9 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 10
Örnek-soru-10 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma ve parantez işlemleri (Kaynak: Supara 9. sınıf):
Örnek Soru - 11
Örnek-soru-11 » Kare kök içinde iki kare farkı şeklinde yazılabilen çarpma ve toplama işlemi ile asal çarpanlarına ayırma (Kaynak: Supara 9. sınıf):
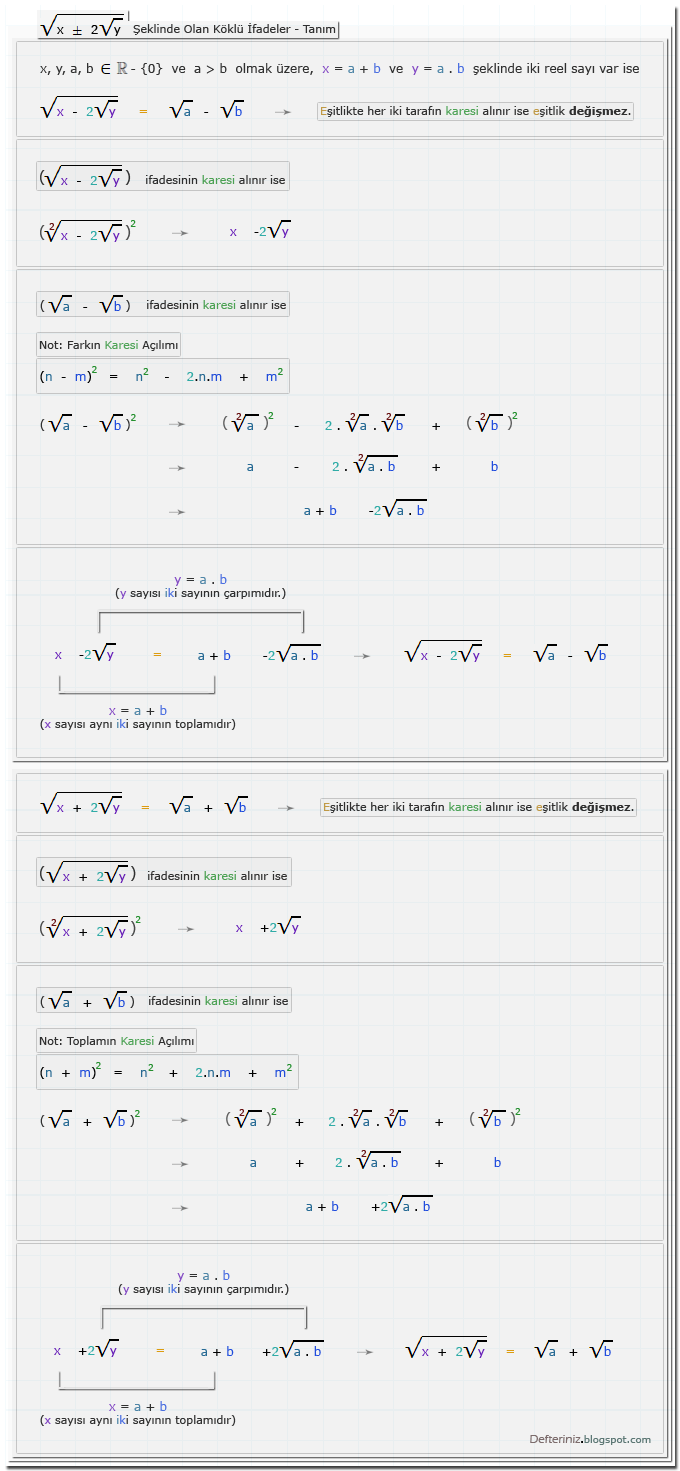
√(x ± 2√y) Şeklinde Olan Köklü İfadeler ve (√a ± √b) Şeklinde Olan İfadelerin Karesi
x, y, a, b ∈ R - {0} ve a > b olmak üzere → x = a + b ve y = a . b şeklinde iki reel sayı var ise
(√x - 2√y) = (√a) - (√b)
(√x + 2√y) = (√a) + (√b)
eşitlikleri yazılabilir.
(√x - 2√y) = (√a) - (√b)
(√x + 2√y) = (√a) + (√b)
eşitlikleri yazılabilir.
√(x ± 2√y) Şeklinde Olan Köklü İfadeler
Tanım » √(x ± 2√y) şeklinde olan köklü ifadelerin tanımı:√(x - 2√y) şeklinde olan köklü ifadeler
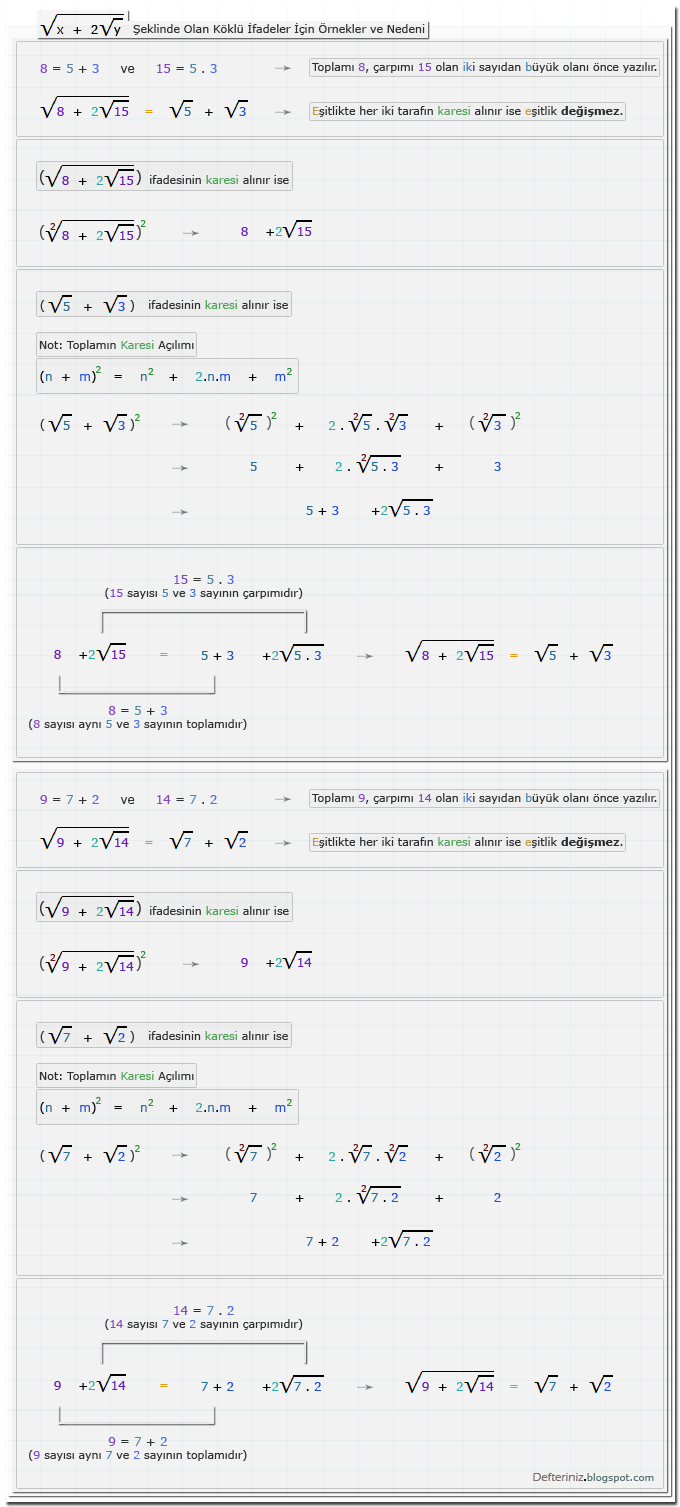
Örnek-29 » √(x - 2√y) şeklinde olan köklü ifadeler ve nedeni ile (√a - √b) şeklinde olan ifadelerin karesi için örnekler:√(x + 2√y) şeklinde olan köklü ifadeler
Örnek-30 » √(x + 2√y) şeklinde olan köklü ifadeler ve nedeni ile (√a + √b) şeklinde olan ifadelerin karesi için örnekler:√(x - 2.z√y) şeklinde olan köklü ifadeler
Örnek-31 » √(x - 2.z√y) şeklinde olan köklü ifadeler ve nedeni ile (√a - √b) şeklinde olan ifadelerin karesi için örnekler:√(x + 2.z√y) şeklinde olan köklü ifadeler
Örnek-32 » √(x + 2.z√y) şeklinde olan köklü ifadeler ve nedeni ile (√a + √b) şeklinde olan ifadelerin karesi için örnekler:√(x - √z.y) şeklinde olan köklü ifadeler
Örnek-33 » √(x - √z.y) şeklinde olan köklü ifadeler ve nedeni ile (√a - √b) şeklinde olan ifadelerin karesi için örnekler:√(x + √z.y) şeklinde olan köklü ifadeler
Örnek-34 » √(x + √z.y) şeklinde olan köklü ifadeler ve nedeni ile (√a + √b) şeklinde olan ifadelerin karesi için örnekler:√(x ± √z.y) şeklinde olan köklü ifadeler
Örnek-35 » √(x ± √z.y) şeklinde olan köklü ifadeler için örnekler:Payda'yı Rasyonel Yapmak, Payda'da √(x ± 2√y) Şeklinde Olan Köklü İfadeler Var İse
√(x ± 2√y) şeklinde köklü ifadeler
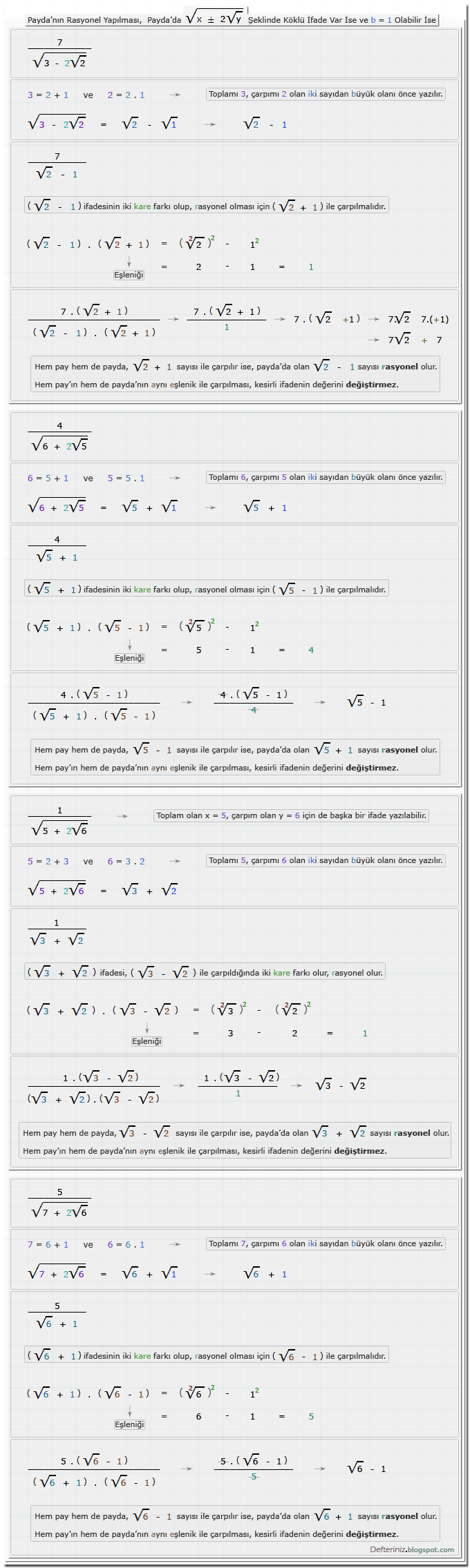
Örnek-36 » Payda'da √(x ± 2√y) şeklinde olan köklü ifadeler var ise ve b = 1 olabilir ise için örnekler:√(x ± 2.z√y) veya √(x ± √z.y) şeklinde köklü ifadeler
Örnek-37 » Payda'da √(x ± 2.z√y) veya √(x ± √z.y) şeklinde olan köklü ifadeler var ise için örnekler:√(x - 2√y) ve √(x + 2√y) şeklinde köklü ifadeler (Soru)
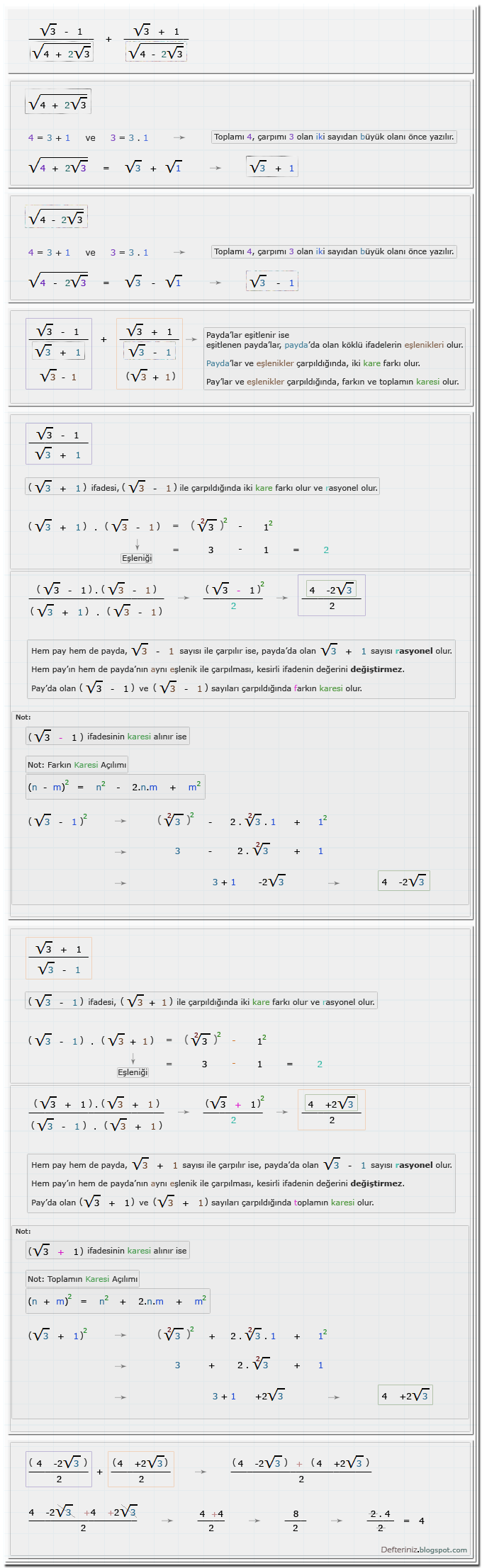
Örnek-38 » Payda'da √(x - 2√y) ve √(x + 2√y) şeklinde olan köklü ifadeler var ise için örnek soru:Örnek Soru - 12
Örnek-soru-12 » Köklü kesirli ifadeler çıkarma işlemi » Payda eşitleme » İki kare farkı, toplamın ve farkın karesi (Kaynak: Supara 9. sınıf):
Örnek Soru - 13
Örnek-soru-13 » Köklü ifadenin eşiti » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: Supara 9. sınıf):
Örnek Soru - 14
Örnek-soru-14 » Köklü ifadenin eşiti » Kök içine giren 2 sayısı ve iki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 15
Örnek-soru-15 » Köklü ifadenin eşiti » Köklü sayının önünde 2 katsayısı » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifade (Kaynak: Supara 9. sınıf):
Örnek Soru - 16
Örnek-soru-16 » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifadelerde çıkarma işlemi » Kök içine giren ve kök dışına çıkan 2 sayısı (Kaynak: Supara 9. sınıf):
Örnek Soru - 17
Örnek-soru-17 » İki sayının toplamı ve çarpımı ile ifade edilen köklü ifadelerde çıkarma işlemi » Kök içine giren ve kök dışına çıkan 2 sayısı (Kaynak: Supara 9. sınıf):
Örnek Soru - 18 » 1. Yol
Örnek-soru-18 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü ifadelerde çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 18 » 2. Yol
Örnek-soru-18 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü ifadelerde çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 19 » 1. Yol
Örnek-soru-19 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadelerde çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 19 » 2. Yol
Örnek-soru-19 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadelerde çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 20
Örnek-soru-20 » Köklü kesirli ifadelerde çıkarma işlemi, Payda'yı rasyonel yapmak ve eşlenikler, İki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 21 » 1. Yol
Örnek-soru-21 » 1. Yol (2/2 ile çarpmak) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadeler, İki kare farkı (Kaynak: Supara 9. sınıf):
Örnek Soru - 21 » 2. Yol
Örnek-soru-21 » 2. Yol (İşlemin karesi) » İki tam sayının toplamı ve çarpımı ile ifade edilemeyen köklü kesirli rasyonel ifadeler, İki kare farkı, Farkın karesi (Kaynak: Supara 9. sınıf):
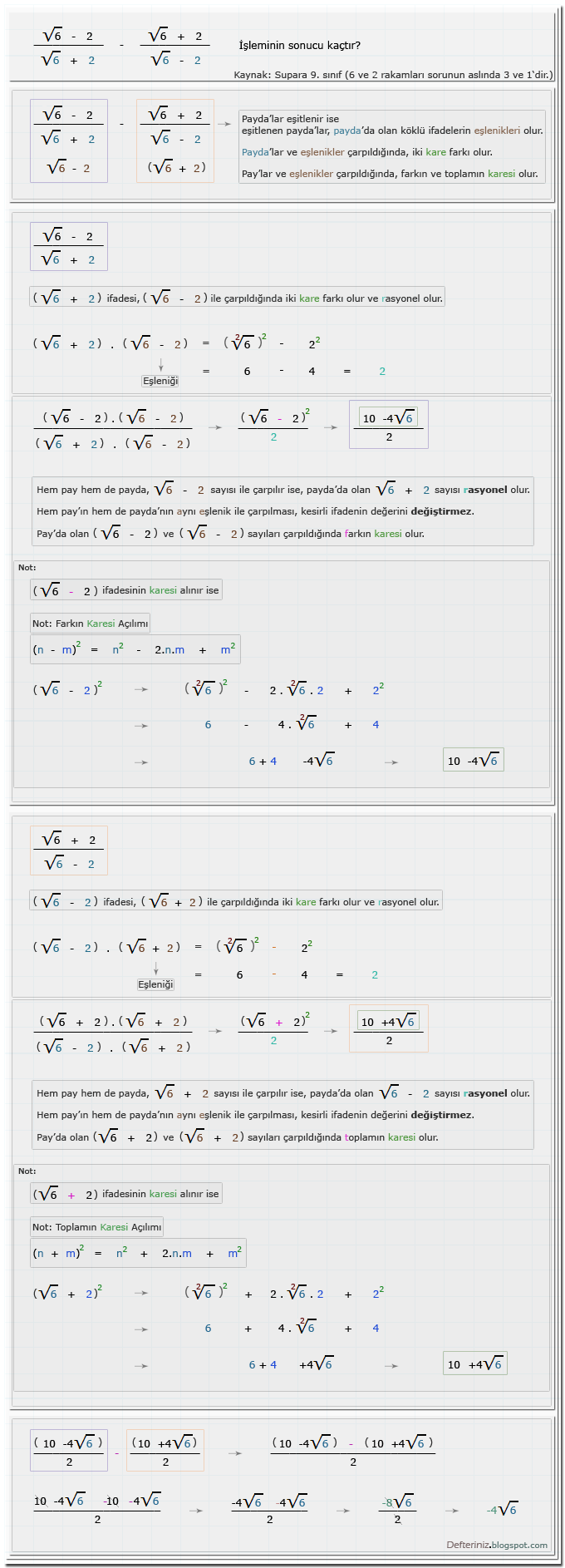
Örnek Soru - 22
Örnek-soru-22 » Köklü Kesirli Rasyonel İfade, İki kare farkı, Farkın karesi, Paranteze alma ve Sadeleşme işlemleri (Kaynak: Supara 9. sınıf):































Yorumlar
Yorum Gönder