Şu an 2. Bölüm görüntüleniyor...
Örnek-2 » Tek dereceden köklü sayıların üslü ifade edilmesi:
Örnek-4 » Tek dereceden köklü sayıların üslü ifade edilmesi » üslü sayıdan köklü sayıya:
Örnek Soru - 1
Örnek-soru-1 » Köklü sayıların üslü ifade edilmesi » eşitliklerden hangileri doğrudur (Kaynak: Supara 9. sınıf):
Örnek-6 » 2. dereceden köklü sayının karesi ve 3. dereceden köklü sayının küpü için örnekler:
Örnek-8 » Üs köklü sayının içine giriyor ise » Köklü sayının önünde katsayı, negatif katsayı veya (-) işaret varsa için örnekler:
Örnek-9 » Üs köklü sayının içine giriyor veya girmiyor ise » Önünde katsayı olmayan veya (-) işaret olabilen örnekler:
Örnek-10 » Köklü sayıların üsleri » Kök içinde üslü işlemler için örnekler:
Örnek-12 » Kare kök ve küp kök dışına çıkan, pay'ında veya payda'sında 1 olan kesirli sayılar için örnekler:
Örnek-13 » Kök içinde kesirli sayıların üslü ifade edilmesi » üslü sayıların kesirli ifade edilmesi için örnekler:
Örnek-15 » 2. ve 4. dereceden kök dışına çıkan, virgülden sonra dört hane (onbinde birler) ondalık sayılar için örnekler:
Örnek-16 » Küp kök dışına çıkan, virgülden sonra üç hane (binde birler) ondalık sayılar için örnekler:
Örnek-17 » Kare kök ve küp kök dışına çıkan, üslü ifade edilen ondalık sayılar için örnekler:
Örnek-19 » Küp kök içine giren kesirli sayılar için örnekler:
Örnek-21 » Küp kök dışına çıkan ve çarpanlarından biri kök içinde kalan kesirli sayılar için örnekler:
Örnek Soru - 2
Örnek-soru-2 » Köklü ondalık sayılar » kare kök, küp kök ve 4. dereceden kök ile çıkarma ve bölme işlemi (Kaynak: Supara 9. sınıf):
Örnek-23 » 3. dereceden küp kök dışına çıkan ve çarpanlarından biri kök içinde kalan ondalık sayılar için örnekler:
Örnek Soru - 3
Örnek-soru-3 » Köklü ondalık sayılar » kök içinde kalan ondalık sayı » köklü sayılarda toplama işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 4
Örnek-soru-4 » Köklü ondalık sayılar » köklü sayılarda toplama ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 5
Örnek-soru-5 » Köklü ondalık sayılar » Çarpma işlemi » x, y, z türünden eşiti hangisidir? (Kaynak: Supara 9. sınıf):
Örnek-25 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » küçükten büyüğe sıralama için örnekler:
Örnek-27 » Köklü sayının derecesini eşitlemek » sadeleştirme yöntemi » küçükten büyüğe sıralama için örnekler:
Örnek Soru - 6
Örnek-soru-6 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » sıralama (Kaynak: Supara 9. sınıf):
Örnek Soru - 7
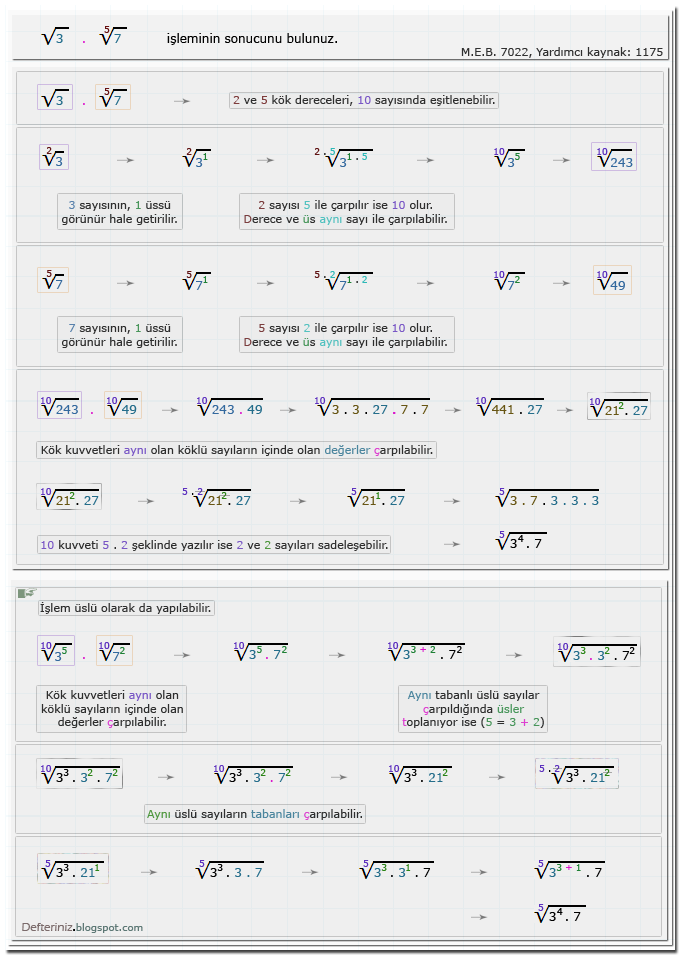
Örnek-soru-7 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » köklü sayılarda çarpma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 8
Örnek-soru-8 » Değeri mutlak değer içinde olan köklü sayılar » tek ve çift dereceden köklü ifadenin eşiti (Kaynak: Supara 9. sınıf):
Örnek Soru - 9
Örnek-soru-9 » Değeri mutlak değer içinde olan köklü sayılar » iç içe kare köklü ifadenin eşiti » 2. dereceden çarpanlara ayırma, tam kare (Kaynak: Supara 9. sınıf):
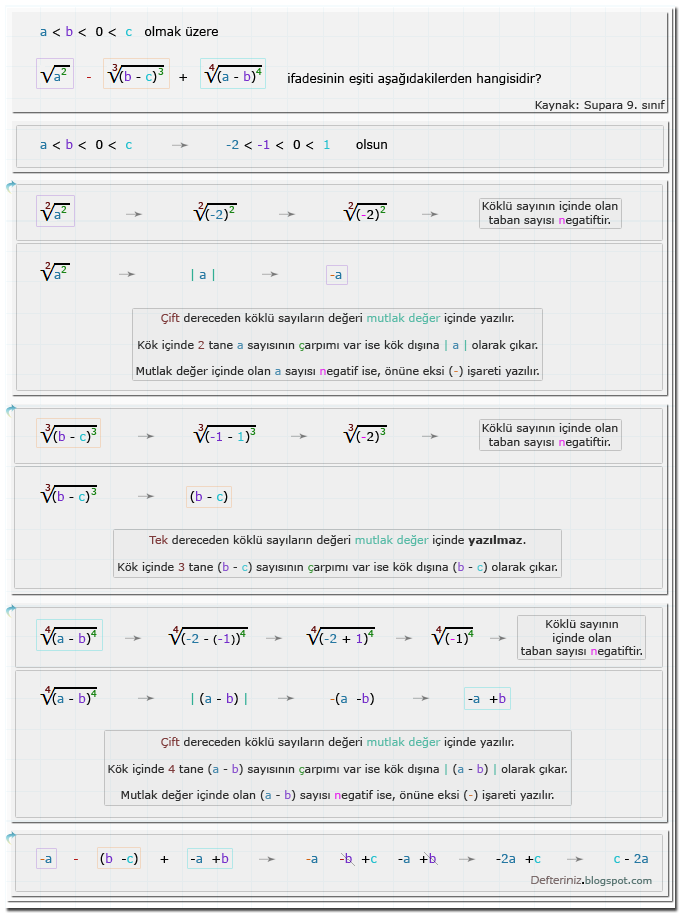
Örnek Soru - 10
Örnek-soru-10 » Değeri mutlak değer içinde olan köklü sayılar » 2 bilinmeyenli köklü ifadeler ile toplama ve çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
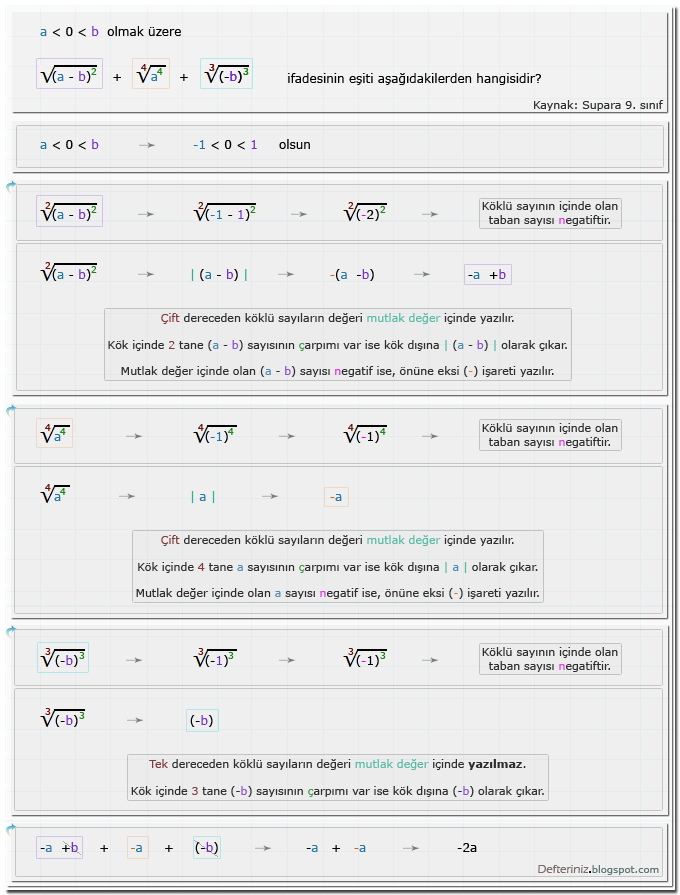
Örnek Soru - 11
Örnek-soru-11 » Değeri mutlak değer içinde olan 3 bilinmeyenli köklü ifadeler ile toplama ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek-29 » İç içe ifade edilen köklü sayılarda a sayısının negatif olabileceği durumlar:
Örnek Soru - 12
Örnek-soru-12 » İç içe ifade edilen 6 tane köklü sayı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
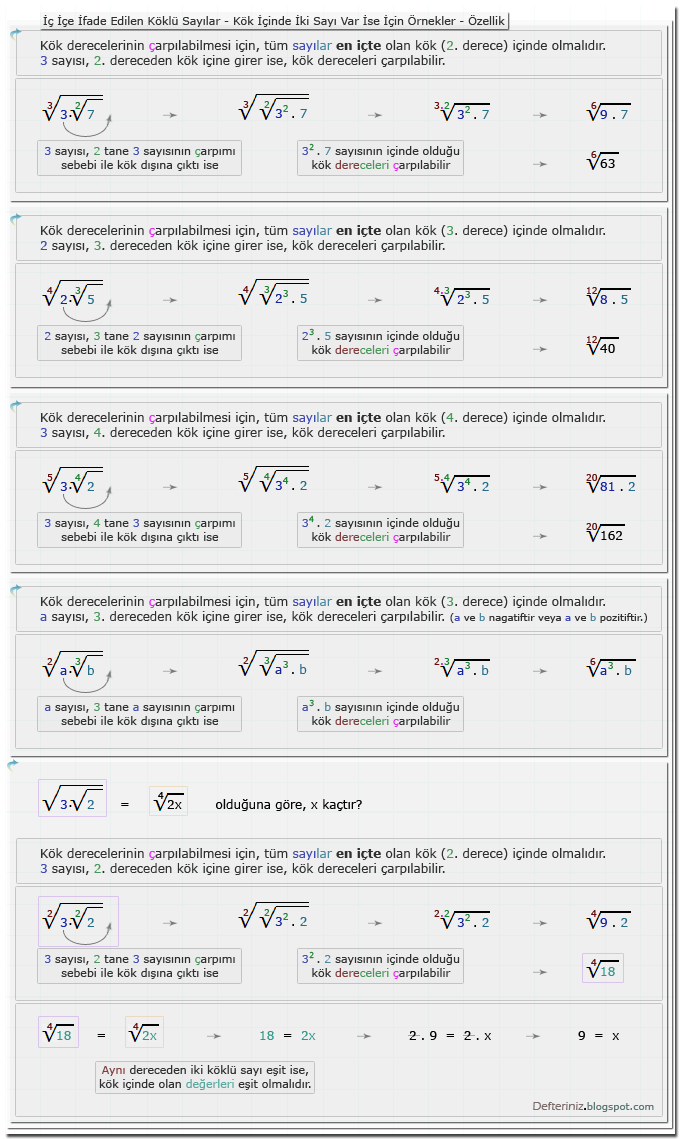
Örnek-29 » İç içe ifade edilen ve kök içinde iki sayı olan köklü sayılar için örnekler:
Örnek-30-1 » İç içe ifade edilen ve kök içinde üç sayı olan köklü sayılar için örnekler - 1:
Örnek-30-2 » İç içe ifade edilen ve kök içinde üç sayı olan köklü sayılar için örnekler - 2:
Örnek Soru - 13
Örnek-soru-13 » İç içe ifade edilen ve kök içinde dört sayı olan köklü sayılar (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 14
Örnek-soru-14 » İç içe ifade edilen üç köklü sayı ve kök derecesinin sadeleşmesi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 15
Örnek-soru-15 » İç içe ifade edilen üç köklü sayı ve kök derecesinin genişletilmesi » köklü denklem (Kaynak: Supara 9. sınıf):
Örnek-31 » Köklü sayılarda toplama ve çıkarma işlemi üslü olarak da yapılabilir için örnekler:
Örnek-32 » Köklü sayılarda olan payda'sı rasyonel kesirli toplama ve çıkarma işlemi, üslü olarak da yapılabilir için örnekler:
Örnek-34 » Köklü (Üslü) sayılarda toplama ve çıkarma işlemi » kök içinde olan değerler eşit değil ise:
Örnek-35 » Köklü sayılarda toplama ve çıkarma işlemi » kök içinde olan değerler eşit değil ise için örnekler:
Örnek Soru - 16
Örnek-soru-16 » Köklü sayılarda toplama ve çıkarma işlemi » Kök dışına çıkan sayılar (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 17
Örnek-soru-17 » Köklü sayılarda toplama işlemi » Küp kök dışına çıkan sayılar » Kesirli sadeleşme işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 18
Örnek-soru-18 » Kare köklü sayılarda toplama ve çıkarma ile kesirli sadeleşme işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 19
Örnek-soru-19 » Köklü sayılarda çıkarma işlemi » Payda'yı kökten kurtarmak (rasyonel yapmak) » Kesirli sadeleşme işlemi (Kaynak: Supara 9. sınıf):
Örnek-37 » Köklü sayılarda çarpma işlemi » Kök kuvveti aynı değil ise » Kök kuvvetini sadeleştirmek:
Örnek Soru - 20
Örnek-soru-20 » Köklü sayılarda çarpma işlemi » Üslü işlemler » Kök kuvvetini sadeleştirmek ve genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 21
Örnek-soru-21 » Köklü sayılarda çarpma işlemi » Üslü işlemler » Kök kuvvetini genişletmek (Kaynak: Supara 9. sınıf):
Örnek Soru - 22
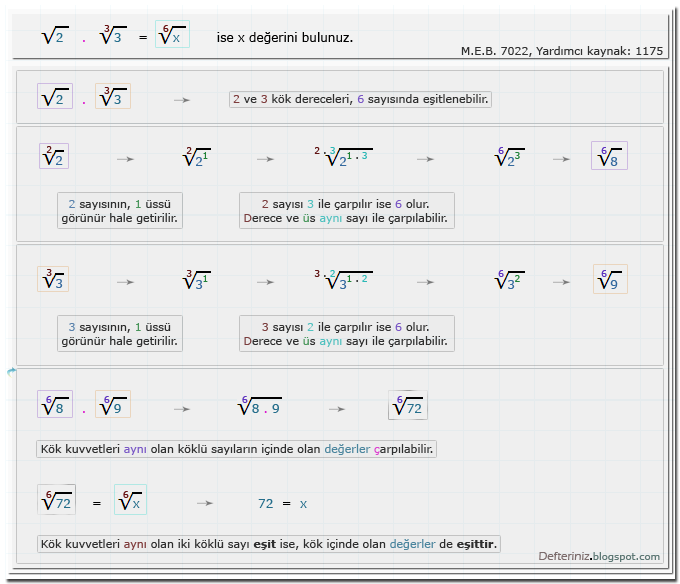
Örnek-soru-22 » Köklü sayılarda çarpma işlemi » Köklü denklem » Kök kuvvetini genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 23
Örnek-soru-23 » Köklü sayılarda çarpma işlemi » İç içe köklü ifadeler » Köklü denklem (Kaynak: Supara 9. sınıf):
Örnek-38 » Köklü sayılarda bölme işlemi » Kök içinde kesirli sayı var ise » Tersten yürütülen işlem örnekleri:
Örnek-40 » Kök kuvveti aynı olmayan köklü sayılarda bölme işlemi » Kök kuvvetinin sadeleştirilmesi:
Örnek Soru - 24
Örnek-soru-24 » Köklü sayılarda bölme işlemi » Kök kuvvetinin genişletmek » Köklü denklem (Kaynak: Supara 9. sınıf):
Köklü Sayıların Özellikleri
Köklü Sayıların Üslü İfade Edilmesi
Tanım » Köklü Sayılar, Kesirli Üslü İfade Edilebilir
a ∈ R ve n ∈ Z⁺ - {1} olmak üzere,
ⁿ√(a üssü m) = ( a üssü (m / n) )
Köklü sayılar, üssü kesirli sayı olan üslü sayı şeklinde ifade edilebilir.
Kök içinde olan a sayısı, taban sayısı olarak yazılır.
Kök içinde olan a sayısının üssü, kesirli üssün pay'ına yazılır.
Köklü sayının derecesi, kesirli üssün payda'sına yazılır.
a sayısı, Reel (Gerçek) sayılar kümesinin elemanıdır.
a sayısı sıfır (0) ise, m sayısı sıfır (0) değildir. a sayısı ve m sayısı sıfır (0) olur ise, kök içinde olan 0⁰ sayısı tanımsız olur.
n sayısı, Pozitif tam sayıları kümesinin, 1 kümesinden farkı kümesinin elemanıdır. Başka bir ifade ile, 1 haricinde olan pozitif tam sayılardır. (2 , 3 , 4 , 5 , ... , ∞)
Tanım » köklü sayılar, üssü kesirli sayı olan üslü sayı şeklinde ifade edilebilir:ⁿ√(a üssü m) = ( a üssü (m / n) )
Köklü sayılar, üssü kesirli sayı olan üslü sayı şeklinde ifade edilebilir.
Kök içinde olan a sayısı, taban sayısı olarak yazılır.
Kök içinde olan a sayısının üssü, kesirli üssün pay'ına yazılır.
Köklü sayının derecesi, kesirli üssün payda'sına yazılır.
a sayısı, Reel (Gerçek) sayılar kümesinin elemanıdır.
a sayısı sıfır (0) ise, m sayısı sıfır (0) değildir. a sayısı ve m sayısı sıfır (0) olur ise, kök içinde olan 0⁰ sayısı tanımsız olur.
n sayısı, Pozitif tam sayıları kümesinin, 1 kümesinden farkı kümesinin elemanıdır. Başka bir ifade ile, 1 haricinde olan pozitif tam sayılardır. (2 , 3 , 4 , 5 , ... , ∞)
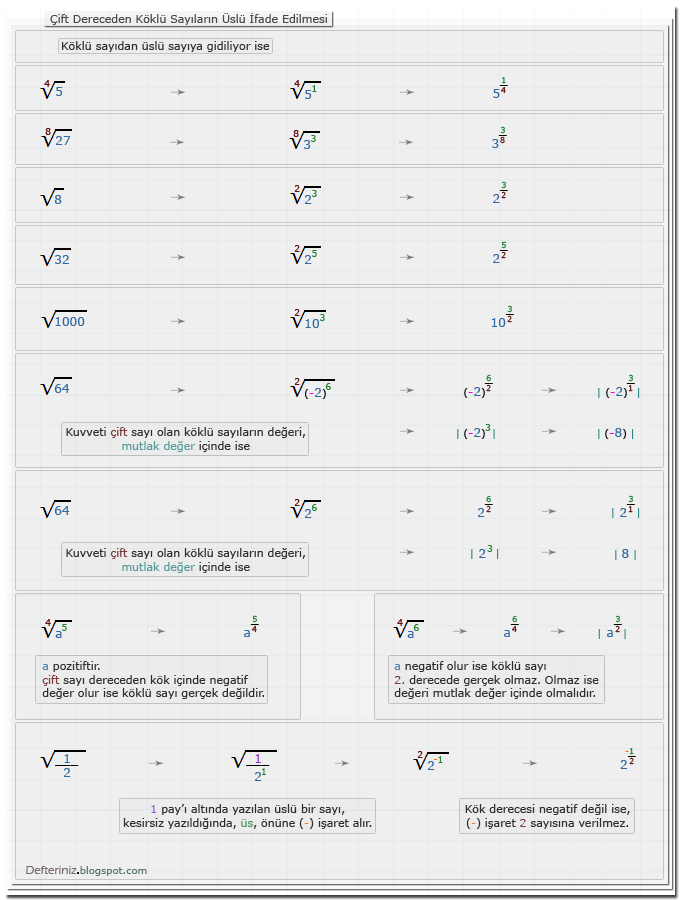
Köklü Sayıdan Üslü Sayıya Gidiliyor İse
Örnek-1 » Çift dereceden köklü sayıların üslü ifade edilmesi:Örnek-2 » Tek dereceden köklü sayıların üslü ifade edilmesi:
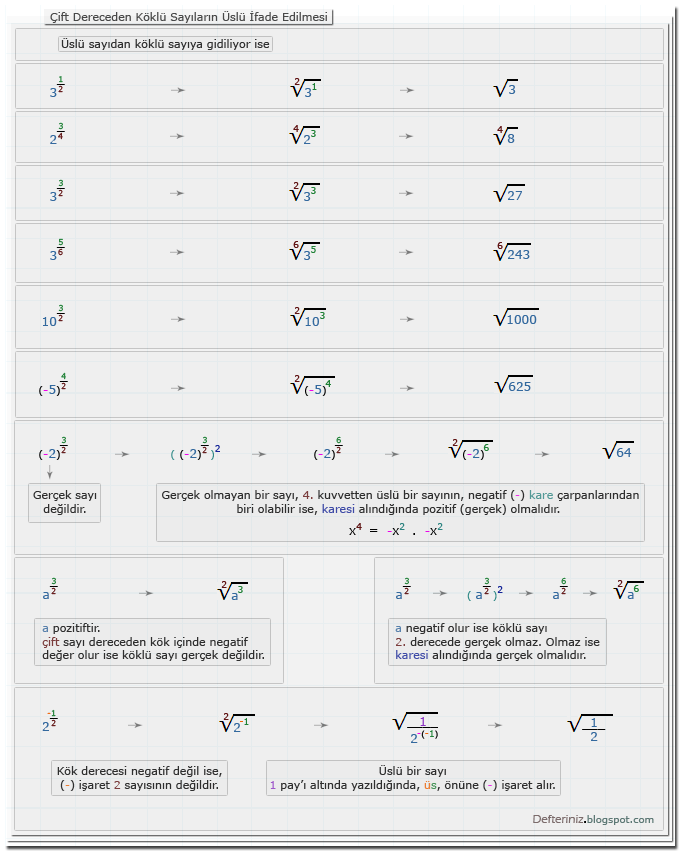
Üslü Sayıdan Köklü Sayıya Gidiliyor İse
Örnek-3 » Çift dereceden köklü sayıların üslü ifade edilmesi » üslü sayıdan köklü sayıya:Örnek-4 » Tek dereceden köklü sayıların üslü ifade edilmesi » üslü sayıdan köklü sayıya:
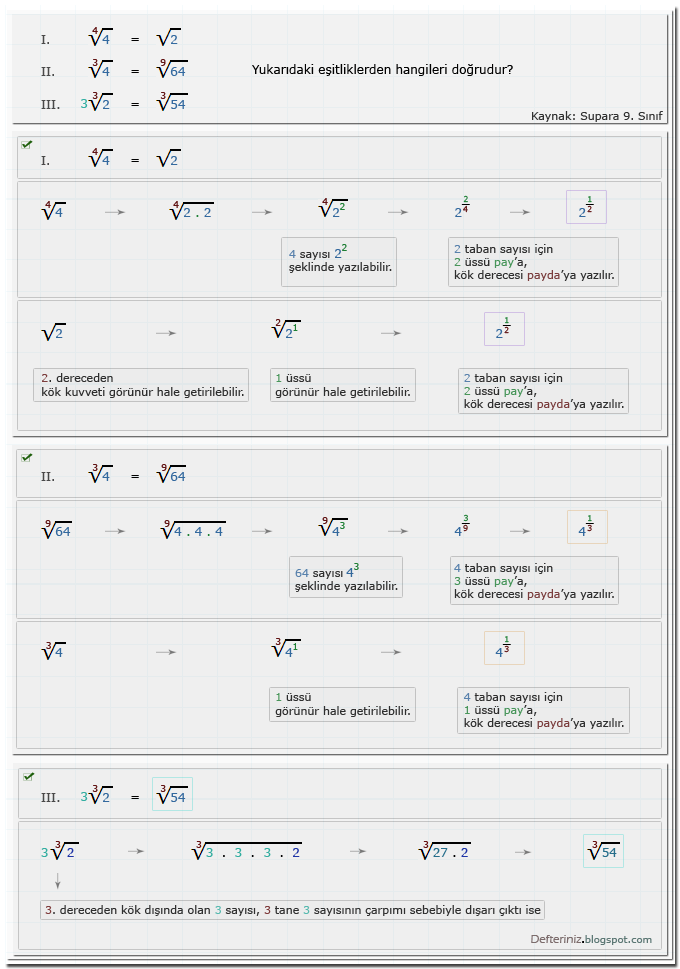
Örnek Soru - 1
Örnek-soru-1 » Köklü sayıların üslü ifade edilmesi » eşitliklerden hangileri doğrudur (Kaynak: Supara 9. sınıf):
Köklü Sayıların Üsleri
Üs Köklü Sayıya Ait İse
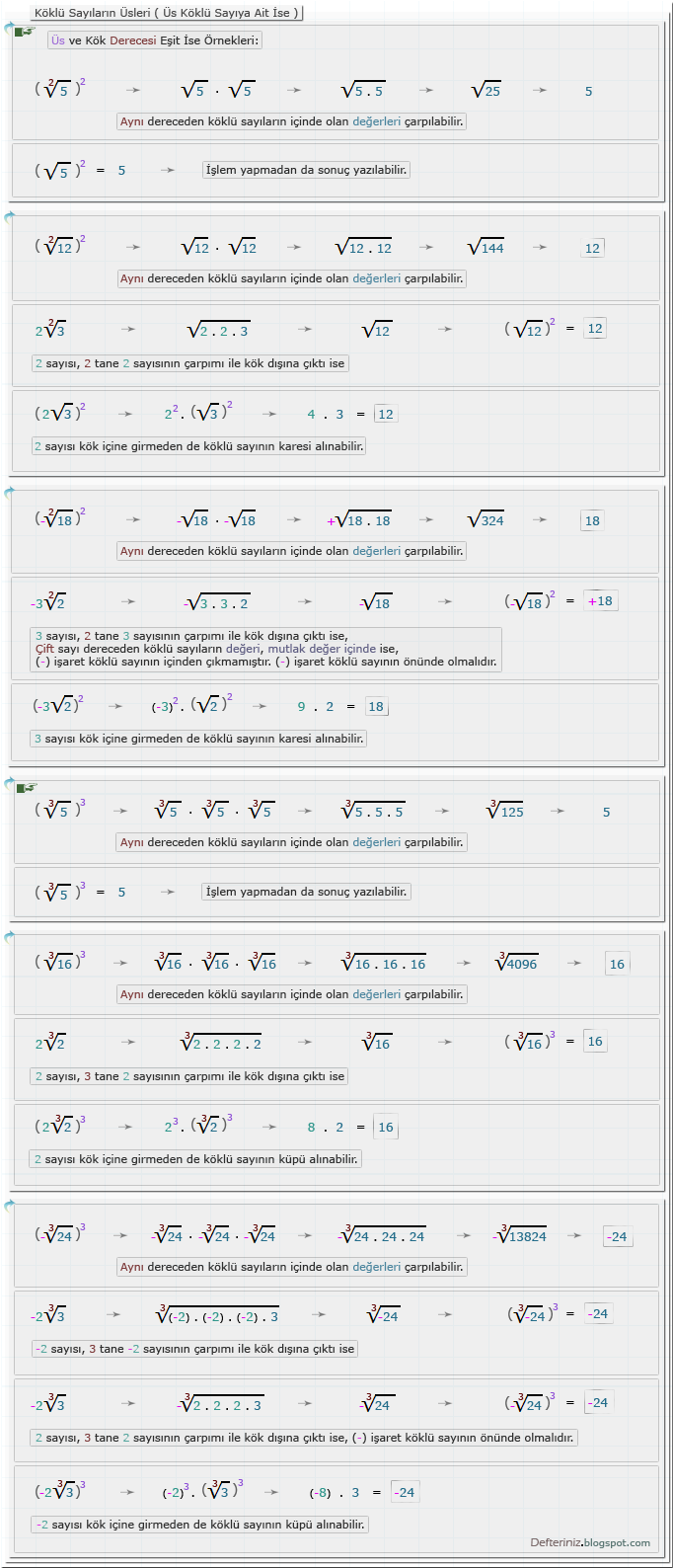
Örnek-5 » Üs köklü sayıya ait ise » Üs ve kök derecesi eşit ise » 2. dereceden köklü sayının karesi ve 3. dereceden köklü sayının küpü:Örnek-6 » 2. dereceden köklü sayının karesi ve 3. dereceden köklü sayının küpü için örnekler:
Üs Köklü Sayıya Ait ise İçinde Olan Değere de Aittir
Örnek-7 » Üs köklü sayıya ait ise içinde olan değere de aittir » Üs ve kök derecesi eşit değil ise:Örnek-8 » Üs köklü sayının içine giriyor ise » Köklü sayının önünde katsayı, negatif katsayı veya (-) işaret varsa için örnekler:
Örnek-9 » Üs köklü sayının içine giriyor veya girmiyor ise » Önünde katsayı olmayan veya (-) işaret olabilen örnekler:
Örnek-10 » Köklü sayıların üsleri » Kök içinde üslü işlemler için örnekler:
Kök İçinde veya Kök Dışında Kesirli Sayı Olabilen Köklü Sayılar
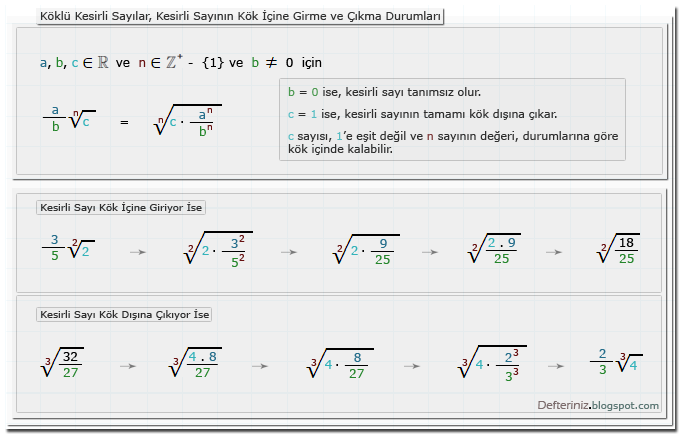
Tanım » Kesirli Sayının Kök İçine Girme veya Çıkma Durumları
a, b, c ∈ R ve n ∈ Z⁺ - {1} ve b ≠ 0 için
(a / b)ⁿ√c = ⁿ√c.(aⁿ / bⁿ)
b = 0 ise, kesirli sayı tanımsız olur.
c = 1 ise, kesirli sayının tamamı kök dışına çıkar.
c sayısı, 1'e eşit değil ve n sayının değeri, durumlarına göre kök içinde kalabilir.
Tanım » Kesirli sayının kök içine girme veya çıkma durumları:(a / b)ⁿ√c = ⁿ√c.(aⁿ / bⁿ)
b = 0 ise, kesirli sayı tanımsız olur.
c = 1 ise, kesirli sayının tamamı kök dışına çıkar.
c sayısı, 1'e eşit değil ve n sayının değeri, durumlarına göre kök içinde kalabilir.
Tamamı Kök Dışına Çıkan Kesirli Sayılar (c = 1 ise)
Örnek-11 » Kare kök ve küp kök dışına çıkan kesirli sayılar için örnekler:Örnek-12 » Kare kök ve küp kök dışına çıkan, pay'ında veya payda'sında 1 olan kesirli sayılar için örnekler:
Örnek-13 » Kök içinde kesirli sayıların üslü ifade edilmesi » üslü sayıların kesirli ifade edilmesi için örnekler:
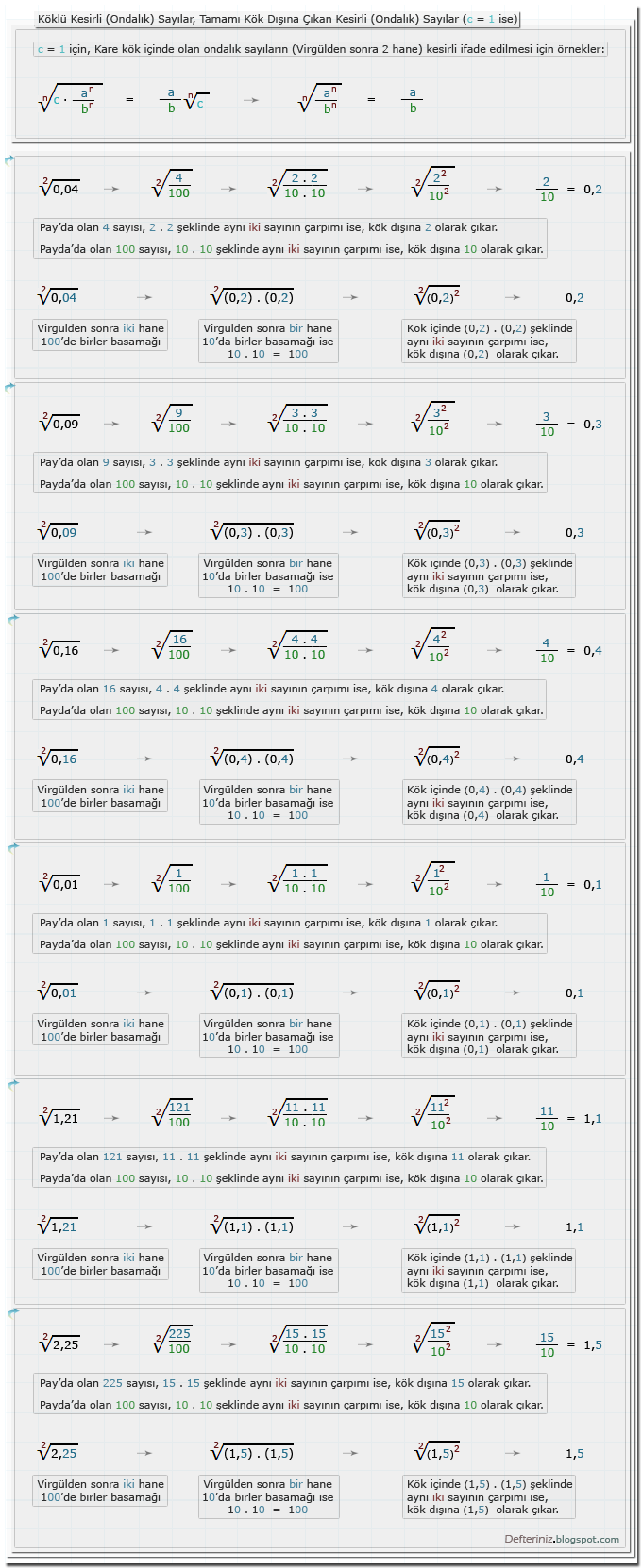
Tamamı Kök Dışına Çıkan Ondalık Sayılar (c = 1 ise)
Örnek-14 » Kare kök dışına çıkan, virgülden sonra iki hane (yüzde birler) ondalık sayılar için örnekler:Örnek-15 » 2. ve 4. dereceden kök dışına çıkan, virgülden sonra dört hane (onbinde birler) ondalık sayılar için örnekler:
Örnek-16 » Küp kök dışına çıkan, virgülden sonra üç hane (binde birler) ondalık sayılar için örnekler:
Örnek-17 » Kare kök ve küp kök dışına çıkan, üslü ifade edilen ondalık sayılar için örnekler:
Kesirli Sayıların Kök İçine Girme Durumları (c ≠ 1 ise)
Örnek-18 » Kare kök içine giren kesirli sayılar için örnekler:Örnek-19 » Küp kök içine giren kesirli sayılar için örnekler:
Kesirli Sayıların Kök Dışına Çıkma Durumları (c ≠ 1 ise)
Örnek-20 » Kare kök dışına çıkan ve çarpanlarından biri kök içinde kalan kesirli sayılar için örnekler:Örnek-21 » Küp kök dışına çıkan ve çarpanlarından biri kök içinde kalan kesirli sayılar için örnekler:
Örnek Soru - 2
Örnek-soru-2 » Köklü ondalık sayılar » kare kök, küp kök ve 4. dereceden kök ile çıkarma ve bölme işlemi (Kaynak: Supara 9. sınıf):
Ondalık Sayıların Kök Dışına Çıkma Durumları (c ≠ 1 ise)
Örnek-22 » Kare kök ve 4. dereceden kök dışına çıkan ve çarpanlarından biri kök içinde kalan ondalık sayılar için örnekler:Örnek-23 » 3. dereceden küp kök dışına çıkan ve çarpanlarından biri kök içinde kalan ondalık sayılar için örnekler:
Örnek Soru - 3
Örnek-soru-3 » Köklü ondalık sayılar » kök içinde kalan ondalık sayı » köklü sayılarda toplama işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 4
Örnek-soru-4 » Köklü ondalık sayılar » köklü sayılarda toplama ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 5
Örnek-soru-5 » Köklü ondalık sayılar » Çarpma işlemi » x, y, z türünden eşiti hangisidir? (Kaynak: Supara 9. sınıf):
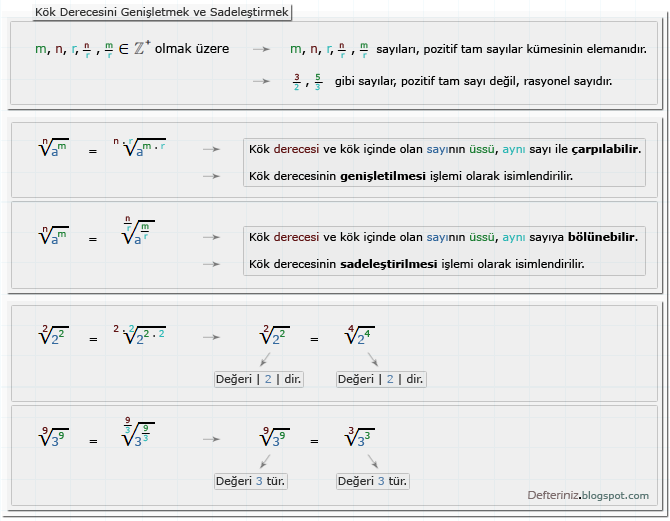
Kök Derecesini Genişletmek ve Sadeleştirmek
m, n, r, (n/r), (m/r) ∈ Z⁺ olmak üzere
n√(a üssü m) = n.r√(a üssü m.r) → Kök derecesi ve kök içinde olan sayının üssü, aynı sayı ile çarpılabilir. Kök derecesinin genişletilmesi işlemi olarak isimlendirilir.
n√(a üssü m) = n/r√(a üssü m/r) → Kök derecesi ve kök içinde olan sayının üssü, aynı sayıya bölünebilir. Kök derecesinin sadeleştirilmesi işlemi olarak isimlendirilir.
Tanım » Kök derecesini genişletmek ve sadeleştirmek:n√(a üssü m) = n.r√(a üssü m.r) → Kök derecesi ve kök içinde olan sayının üssü, aynı sayı ile çarpılabilir. Kök derecesinin genişletilmesi işlemi olarak isimlendirilir.
n√(a üssü m) = n/r√(a üssü m/r) → Kök derecesi ve kök içinde olan sayının üssü, aynı sayıya bölünebilir. Kök derecesinin sadeleştirilmesi işlemi olarak isimlendirilir.
Kök Derecesini Genişletmek
Örnek-24 » Tek ve çift dereceden kök derecesini genişletme için örnekler:Örnek-25 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » küçükten büyüğe sıralama için örnekler:
Kök Derecesini Sadeleştirmek
Örnek-26 » Tek ve çift dereceden kök derecesini sadeleştirme için örnekler:Örnek-27 » Köklü sayının derecesini eşitlemek » sadeleştirme yöntemi » küçükten büyüğe sıralama için örnekler:
Kök Derecesi İçin Genişleme ve Sadeleşme Yapılmaması Gereken Durumlar
Örnek-28 » Kök derecesi için genişleme ve sadeleşme yapılmaması gereken durumlar:Örnek Soru - 6
Örnek-soru-6 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » sıralama (Kaynak: Supara 9. sınıf):
Örnek Soru - 7
Örnek-soru-7 » Köklü sayının derecesini eşitlemek » genişletme yöntemi » köklü sayılarda çarpma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
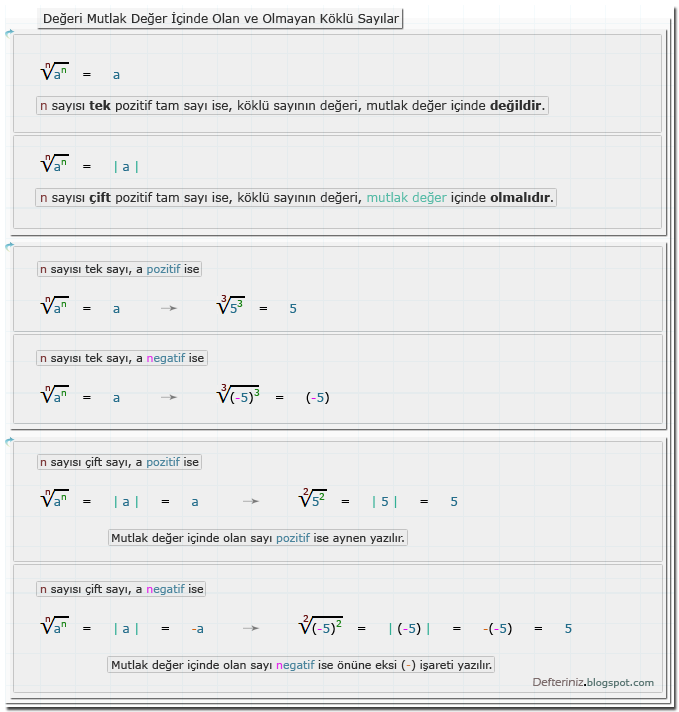
Değeri Mutlak Değer İçinde Olan ve Olmayan Köklü Sayılar
n sayısı tek pozitif tam sayı ise, köklü sayının değeri, mutlak değer içinde değildir.
ⁿ√aⁿ = a
n sayısı çift pozitif tam sayı ise, köklü sayının değeri, mutlak değer içinde olmalıdır.
ⁿ√aⁿ = | a |
Tanım » Değeri mutlak değer içinde olan ve olmayan, içinde negatif ve pozitif taban sayısı olabilen köklü sayılar:ⁿ√aⁿ = a
n sayısı çift pozitif tam sayı ise, köklü sayının değeri, mutlak değer içinde olmalıdır.
ⁿ√aⁿ = | a |
Örnek Soru - 8
Örnek-soru-8 » Değeri mutlak değer içinde olan köklü sayılar » tek ve çift dereceden köklü ifadenin eşiti (Kaynak: Supara 9. sınıf):
Örnek Soru - 9
Örnek-soru-9 » Değeri mutlak değer içinde olan köklü sayılar » iç içe kare köklü ifadenin eşiti » 2. dereceden çarpanlara ayırma, tam kare (Kaynak: Supara 9. sınıf):
Örnek Soru - 10
Örnek-soru-10 » Değeri mutlak değer içinde olan köklü sayılar » 2 bilinmeyenli köklü ifadeler ile toplama ve çıkarma işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 11
Örnek-soru-11 » Değeri mutlak değer içinde olan 3 bilinmeyenli köklü ifadeler ile toplama ve çıkarma işlemi (Kaynak: Supara 9. sınıf):
İç İçe İfade Edilen Köklü Sayılar
Kök İçinde Bir Tane Sayı Var İse
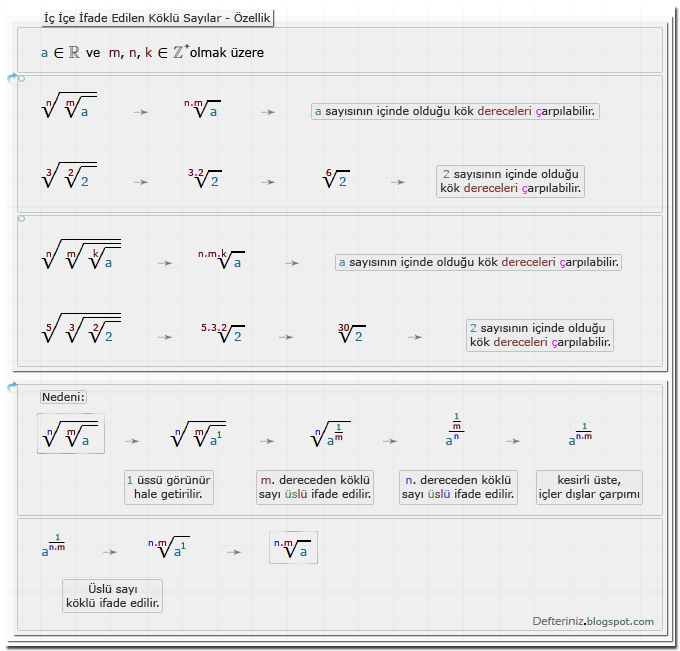
a ∈ R ve m, n, k ∈ Z⁺ olmak üzere
n√m√k√a = n.m.k√a → a sayısının içinde olduğu kök dereceleri çarpılabilir.
Tanım » İç içe ifade edilen ve kök içinde bir tane sayı olan köklü sayılar:n√m√k√a = n.m.k√a → a sayısının içinde olduğu kök dereceleri çarpılabilir.
Örnek-29 » İç içe ifade edilen köklü sayılarda a sayısının negatif olabileceği durumlar:
Örnek Soru - 12
Örnek-soru-12 » İç içe ifade edilen 6 tane köklü sayı (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Kök İçinde 1'den Çok Sayı Var İse
Tanım » İç içe ifade edilen ve kök içinde 1'den çok sayı olan köklü sayılar:Örnek-29 » İç içe ifade edilen ve kök içinde iki sayı olan köklü sayılar için örnekler:
Örnek-30-1 » İç içe ifade edilen ve kök içinde üç sayı olan köklü sayılar için örnekler - 1:
Örnek-30-2 » İç içe ifade edilen ve kök içinde üç sayı olan köklü sayılar için örnekler - 2:
Örnek Soru - 13
Örnek-soru-13 » İç içe ifade edilen ve kök içinde dört sayı olan köklü sayılar (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 14
Örnek-soru-14 » İç içe ifade edilen üç köklü sayı ve kök derecesinin sadeleşmesi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 15
Örnek-soru-15 » İç içe ifade edilen üç köklü sayı ve kök derecesinin genişletilmesi » köklü denklem (Kaynak: Supara 9. sınıf):
Köklü Sayılarda Toplama ve Çıkarma İşlemi
Kök İçinde Olan Değerler Eşit İse
a ∈ R ve n ∈ Z⁺ - {1} olmak üzere,
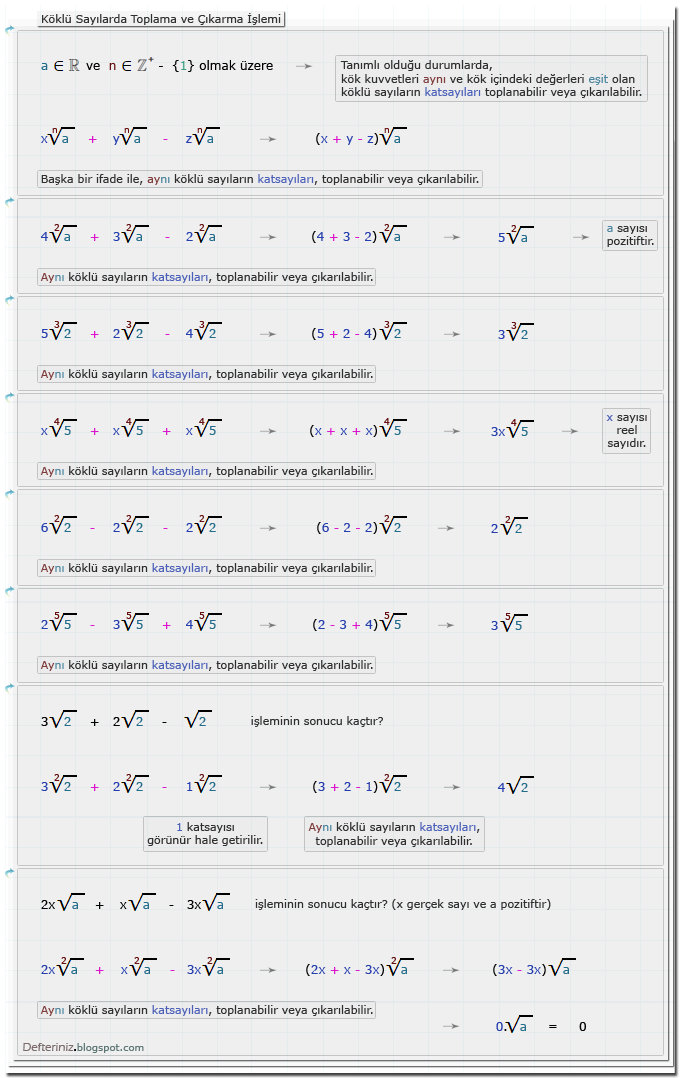
tanımlı olduğu durumlarda, kök kuvvetleri aynı ve kök içindeki değerleri eşit olan köklü sayıların katsayıları toplanabilir veya çıkarılabilir.
xn√a + yn√a - zn√a = (x + y - z)n√a
Başka bir ifade ile, aynı köklü sayıların katsayıları, toplanabilir veya çıkarılabilir.
Tanım » Köklü sayılarda toplama ve çıkarma işlemi:tanımlı olduğu durumlarda, kök kuvvetleri aynı ve kök içindeki değerleri eşit olan köklü sayıların katsayıları toplanabilir veya çıkarılabilir.
xn√a + yn√a - zn√a = (x + y - z)n√a
Başka bir ifade ile, aynı köklü sayıların katsayıları, toplanabilir veya çıkarılabilir.
Örnek-31 » Köklü sayılarda toplama ve çıkarma işlemi üslü olarak da yapılabilir için örnekler:
Örnek-32 » Köklü sayılarda olan payda'sı rasyonel kesirli toplama ve çıkarma işlemi, üslü olarak da yapılabilir için örnekler:
Kök İçinde Olan Değerler Eşit Değil İse Değerleri Eşitlemek
Örnek-33 » Köklü sayılarda toplama ve çıkarma işlemi » kök içinde olan değerler eşit değil ise » değerleri eşitlemek:Örnek-34 » Köklü (Üslü) sayılarda toplama ve çıkarma işlemi » kök içinde olan değerler eşit değil ise:
Örnek-35 » Köklü sayılarda toplama ve çıkarma işlemi » kök içinde olan değerler eşit değil ise için örnekler:
Örnek Soru - 16
Örnek-soru-16 » Köklü sayılarda toplama ve çıkarma işlemi » Kök dışına çıkan sayılar (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 17
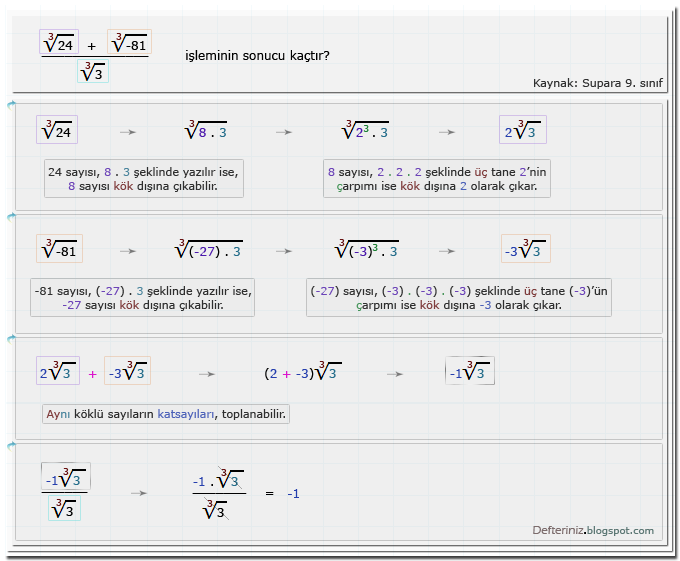
Örnek-soru-17 » Köklü sayılarda toplama işlemi » Küp kök dışına çıkan sayılar » Kesirli sadeleşme işlemi (Kaynak: Supara 9. sınıf):
Örnek Soru - 18
Örnek-soru-18 » Kare köklü sayılarda toplama ve çıkarma ile kesirli sadeleşme işlemi (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 19
Örnek-soru-19 » Köklü sayılarda çıkarma işlemi » Payda'yı kökten kurtarmak (rasyonel yapmak) » Kesirli sadeleşme işlemi (Kaynak: Supara 9. sınıf):
Köklü Sayılarda Çarpma İşlemi
Kök Kuvveti Aynı İse
a, b ∈ R ve n ∈ Z⁺ - {1} olmak üzere,
tanımlı olduğu durumlarda, kök kuvvetleri aynı olan köklü ifadeler çarpılabilir.
n√a . n√b → n√a.b
Başka bir ifade ile, kök kuvvetleri aynı olan köklü sayıların içinde olan değerler çarpılabilir.
Tanım » Kök kuvveti aynı olan köklü sayılarda çarpma işlemi:tanımlı olduğu durumlarda, kök kuvvetleri aynı olan köklü ifadeler çarpılabilir.
n√a . n√b → n√a.b
Başka bir ifade ile, kök kuvvetleri aynı olan köklü sayıların içinde olan değerler çarpılabilir.
Kök Kuvveti Aynı Değil İse
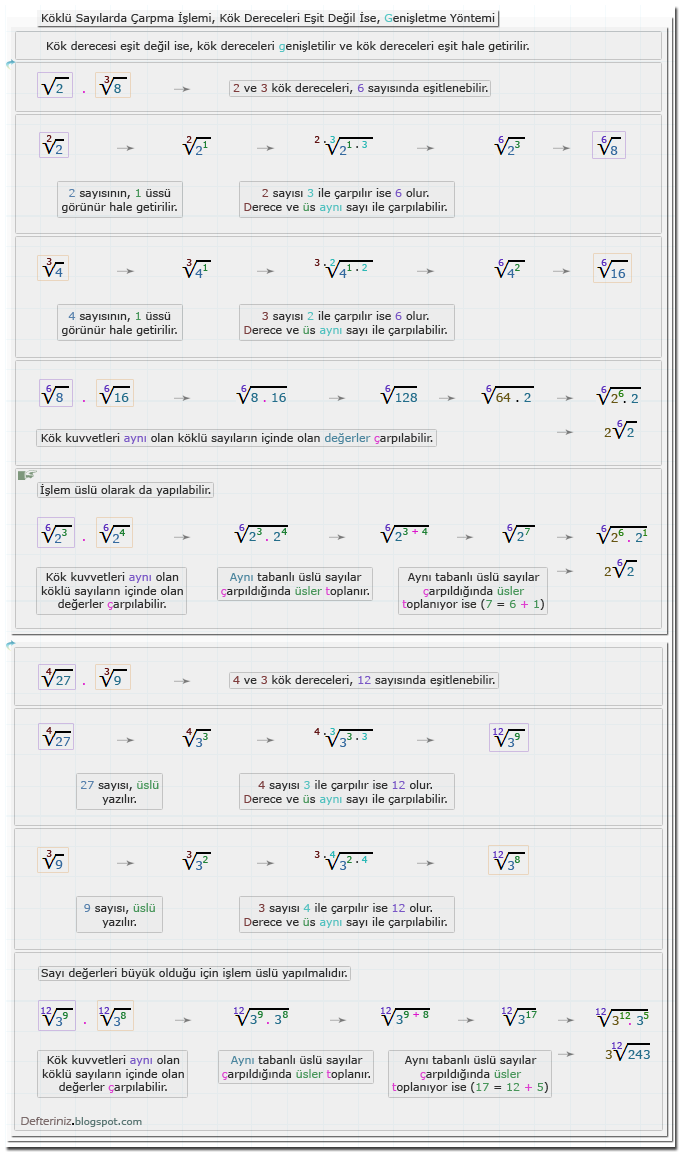
Örnek-36 » Köklü sayılarda çarpma işlemi » Kök kuvveti aynı değil ise » Kök kuvvetini genişletmek:Örnek-37 » Köklü sayılarda çarpma işlemi » Kök kuvveti aynı değil ise » Kök kuvvetini sadeleştirmek:
Örnek Soru - 20
Örnek-soru-20 » Köklü sayılarda çarpma işlemi » Üslü işlemler » Kök kuvvetini sadeleştirmek ve genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 21
Örnek-soru-21 » Köklü sayılarda çarpma işlemi » Üslü işlemler » Kök kuvvetini genişletmek (Kaynak: Supara 9. sınıf):
Örnek Soru - 22
Örnek-soru-22 » Köklü sayılarda çarpma işlemi » Köklü denklem » Kök kuvvetini genişletmek (Kaynak: M.E.B. 7022 , yardımcı kaynak kitap 1175):
Örnek Soru - 23
Örnek-soru-23 » Köklü sayılarda çarpma işlemi » İç içe köklü ifadeler » Köklü denklem (Kaynak: Supara 9. sınıf):
Köklü Sayılarda Bölme İşlemi
Kök Kuvveti Aynı İse
a, b ∈ R ve n ∈ Z⁺ - {1} ve b ≠ 0 olmak üzere,
tanımlı olduğu durumlarda, kök kuvvetleri aynı olan köklü ifadeler bölünebilir.
n√a / n√b → n√a/b
Başka bir ifade ile, kök kuvvetleri aynı olan köklü sayıların içinde olan değerler bölünebilir, kesirli yazılabilir.
Tanım » Kök kuvveti aynı olan köklü sayılarda bölme işlemi:tanımlı olduğu durumlarda, kök kuvvetleri aynı olan köklü ifadeler bölünebilir.
n√a / n√b → n√a/b
Başka bir ifade ile, kök kuvvetleri aynı olan köklü sayıların içinde olan değerler bölünebilir, kesirli yazılabilir.
Örnek-38 » Köklü sayılarda bölme işlemi » Kök içinde kesirli sayı var ise » Tersten yürütülen işlem örnekleri:
Kök Kuvveti Aynı Değil İse
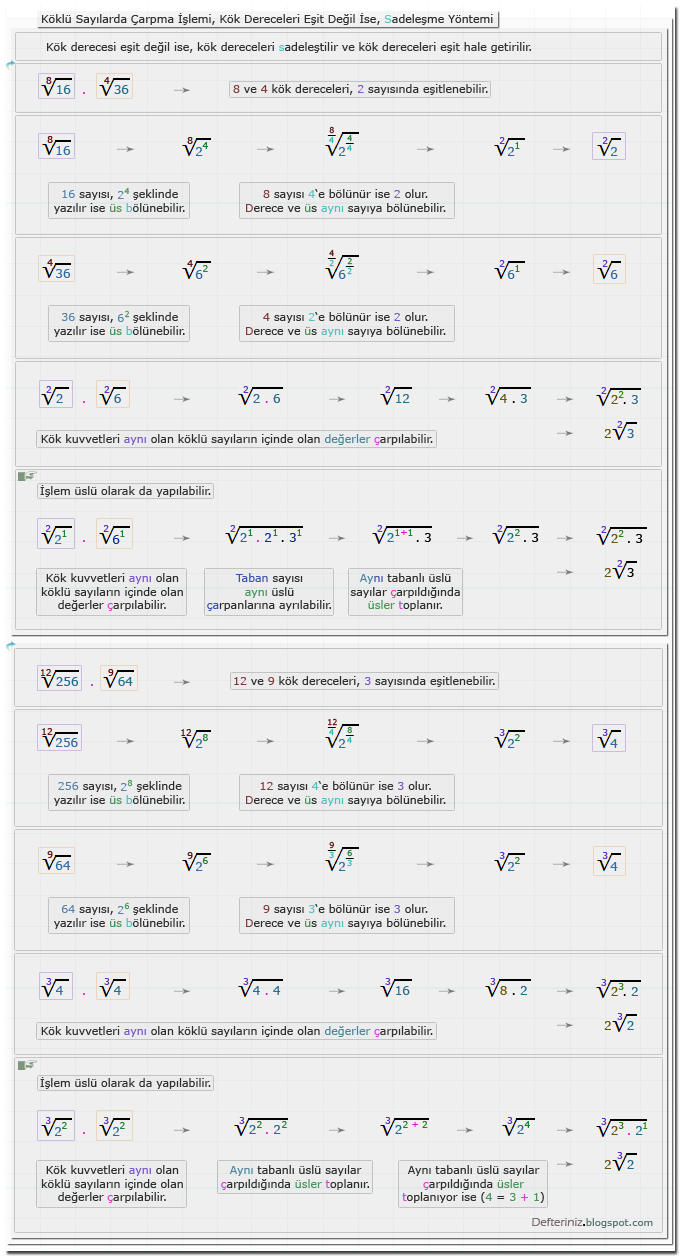
Örnek-39 » Kök kuvveti aynı olmayan köklü sayılarda bölme işlemi » Kök kuvvetinin genişletilmesi:Örnek-40 » Kök kuvveti aynı olmayan köklü sayılarda bölme işlemi » Kök kuvvetinin sadeleştirilmesi:
Örnek Soru - 24
Örnek-soru-24 » Köklü sayılarda bölme işlemi » Kök kuvvetinin genişletmek » Köklü denklem (Kaynak: Supara 9. sınıf):
Not:
Payda'nın rasyonel yapılması ve eşlenikler konusuna 3. bölümde değinilmiştir...
Payda'nın rasyonel yapılması ve eşlenikler konusuna 3. bölümde değinilmiştir...

























































Yorumlar
Yorum Gönder