Şu an 4. Bölüm görüntüleniyor...
Örnek:
İfade bir sayıdan küçük ise » | x | < 5:
Örnek:
İfade bir sayıya küçük eşit ise » | x | ≤ 5:
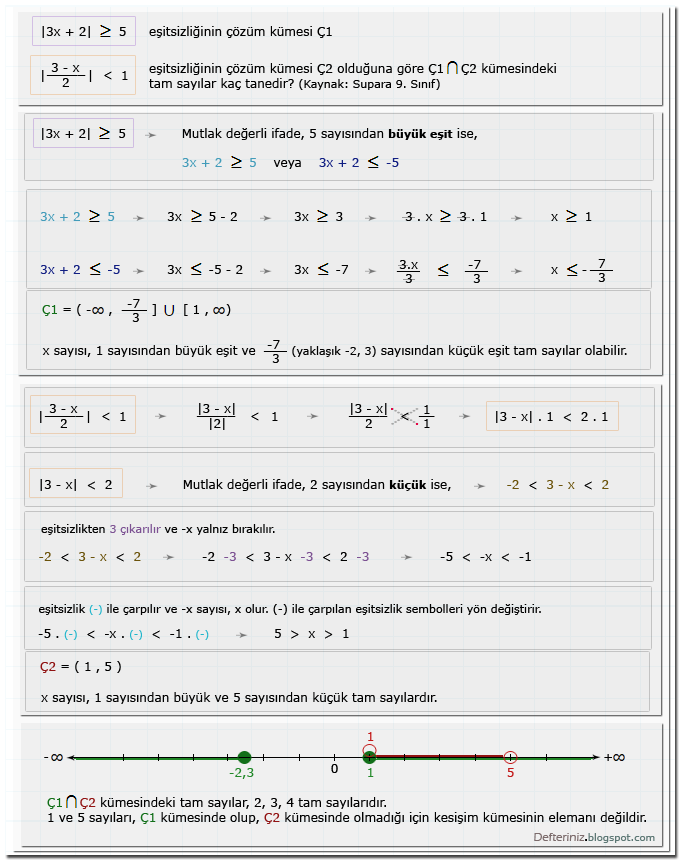
Örnek soru-1:
Mutlak değerli eşitsizlik » Örnek soru-1 » İfade bir sayıdan küçük eşit ise (kaynak: Supara 9. sınıf):
Örnek soru-2:
Mutlak değerli eşitsizlik » Örnek soru-2 » Kesirli ifade sıfırdan küçük ise (kaynak: Supara 9. sınıf):
Mutlak değerli eşitsizlik » Örnek soru-3 » İfade sıfırdan küçük ise (kaynak: Supara 9. sınıf):
Örnek:
İfade bir sayıdan büyük ise » | x | > 5:
Örnek:
İfade bir sayıdan büyük eşit ise » | x | ≥ 5:
Örnek soru-4:
Mutlak değerli eşitsizlik » Örnek soru-4 » İfade bir sayıdan büyük eşit ise (kaynak: Supara 9. sınıf):
Örnek soru-5:
Mutlak değerli eşitsizlik » Örnek soru-5 » İki İfadenin Çözüm Kümesi Kesişimi (kaynak: Supara 9. sınıf):
Örnek soru-6:
Mutlak değerli eşitsizlik » Örnek soru-6 » İfade bir sayıdan büyük ise (kaynak: Supara 9. sınıf):
Örnek:
İfade 2 sayısından büyük, 5 sayısından küçük ise » 2 < | x | < 5:
Örnek:
İfade 2 sayısından büyük eşit, 5 sayısından küçük ise » 2 ≤ | x | < 5:
Örnek:
İfade 2 sayısından büyük, 5 sayısından küçük eşit ise » 2 < | x | ≤ 5:
Örnek:
İfade 2 sayısından büyük eşit, 5 sayısından küçük eşit ise » 2 ≤ | x | ≤ 5:
Örnek soru-7:
Mutlak değerli eşitsizlik » Örnek soru-7 » İfade bir sayıdan büyük eşit diğerinden küçük ise (kaynak: Supara 9. sınıf):
Örnek soru-8:
Mutlak değerli eşitsizlik » Örnek soru-8 » İfade bir sayıdan büyük eşit diğerinden küçük ise (kaynak: Supara 9. sınıf):
Örnek soru-9:
Mutlak değerli eşitsizlik » Örnek soru-9 » İki tarafında mutlak değerli ifade olan eşitsizlikler (kaynak: Supara 9. sınıf):
Mutlak değerli eşitsizlik » Örnek soru-10 » (x, y) Sıralı İkilileri » Analitik (Koordinat) Düzlem (kaynak: M.E.B. Yayınları: 7022):
Mutlak Değerli Eşitsizlikler
Mutlak değerli ifade bulunan eşitsizliklere, mutlak değerli eşitsizlik denir.İfade Bir Sayıdan Küçük İse » | x | < a
a ≥ 0 olmak üzere
| x | < a ise
-a < x < a
a sayısı, sıfıra eşit veya büyük olmak üzere → a ≥ 0
İfade a sayısından küçük ise → | x | < a
a sayısı sıfırdan küçük olsaydı, mutlak değerli ifade sıfırdan küçük olurdu. Mutlak değerli ifade sıfırdan küçük değildir.
x sayısı, -a ile a sayıları arasında değer alabilir → -a < x < a → (-a , a)
Eşitsizlik küçüktür eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahil değildir.
Küçük eşit eşitsizliği ile yazılmış olsaydı, -a ve a sayıları değer aralığına dahil olurdu.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olmadığı için, parantez (-a , a) içine yazılır ve sayı doğrusu üzerinde, içi boş çember (⚪) ile gösterilir.
İfade bir sayıdan küçük ise » | x | < a:| x | < a ise
-a < x < a
a sayısı, sıfıra eşit veya büyük olmak üzere → a ≥ 0
İfade a sayısından küçük ise → | x | < a
a sayısı sıfırdan küçük olsaydı, mutlak değerli ifade sıfırdan küçük olurdu. Mutlak değerli ifade sıfırdan küçük değildir.
x sayısı, -a ile a sayıları arasında değer alabilir → -a < x < a → (-a , a)
Eşitsizlik küçüktür eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahil değildir.
Küçük eşit eşitsizliği ile yazılmış olsaydı, -a ve a sayıları değer aralığına dahil olurdu.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olmadığı için, parantez (-a , a) içine yazılır ve sayı doğrusu üzerinde, içi boş çember (⚪) ile gösterilir.
Örnek:
İfade bir sayıdan küçük ise » | x | < 5:
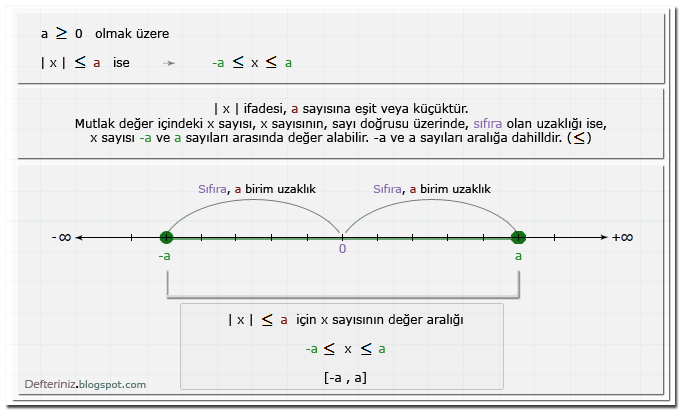
İfade Bir Sayıya Küçük Eşit İse » | x | ≤ a
a ≥ 0 olmak üzere
| x | ≤ a ise
-a ≤ x ≤ a
x sayısı, -a ile a sayıları arasında değer alabilir → -a ≤ x ≤ a → [-a , a]
Eşitsizlik küçük eşit eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahildir.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olduğu için, köşeli parantez [-a , a] içine yazılır ve sayı doğrusu üzerinde, içi dolu daire (⚫) ile gösterilir.
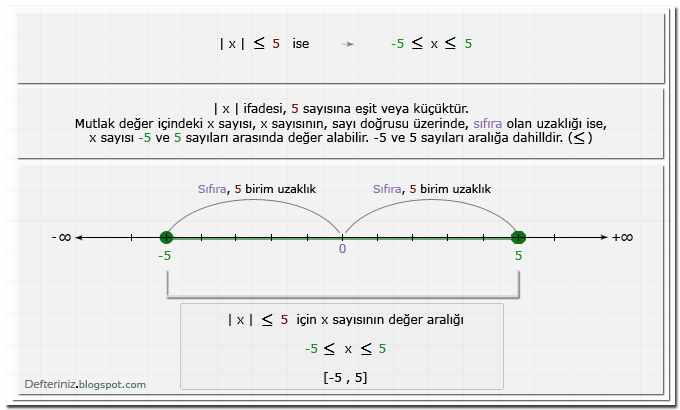
İfade bir sayıya küçük eşit ise » | x | ≤ a:| x | ≤ a ise
-a ≤ x ≤ a
x sayısı, -a ile a sayıları arasında değer alabilir → -a ≤ x ≤ a → [-a , a]
Eşitsizlik küçük eşit eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahildir.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olduğu için, köşeli parantez [-a , a] içine yazılır ve sayı doğrusu üzerinde, içi dolu daire (⚫) ile gösterilir.
Örnek:
İfade bir sayıya küçük eşit ise » | x | ≤ 5:
Örnek soru-1:
Mutlak değerli eşitsizlik » Örnek soru-1 » İfade bir sayıdan küçük eşit ise (kaynak: Supara 9. sınıf):
Örnek soru-2:
Mutlak değerli eşitsizlik » Örnek soru-2 » Kesirli ifade sıfırdan küçük ise (kaynak: Supara 9. sınıf):
İfade Sıfırdan Küçük İse » | x | < a (a < 0)
a < 0 olmak üzere
| x | < a ise
Eşitsizliğin çözüm kümesi boş kümedir.
a sayısı, sıfırdan küçük üzere → a < 0
İfade a sayısından küçük ise → | x | < a
Mutlak değerli bir ifadenin alabileceği en küçük değer sıfırdır. a sayısı sıfırdan küçük ise, mutlak değerli |x| ifadesi de sıfırdan küçük olur. Mutlak değerli bir ifade negatif değildir. Eşitsizliğin çözüm kümesi boş kümedir.
Ç = ∅
Örnek soru-3:| x | < a ise
Eşitsizliğin çözüm kümesi boş kümedir.
a sayısı, sıfırdan küçük üzere → a < 0
İfade a sayısından küçük ise → | x | < a
Mutlak değerli bir ifadenin alabileceği en küçük değer sıfırdır. a sayısı sıfırdan küçük ise, mutlak değerli |x| ifadesi de sıfırdan küçük olur. Mutlak değerli bir ifade negatif değildir. Eşitsizliğin çözüm kümesi boş kümedir.
Ç = ∅
Mutlak değerli eşitsizlik » Örnek soru-3 » İfade sıfırdan küçük ise (kaynak: Supara 9. sınıf):
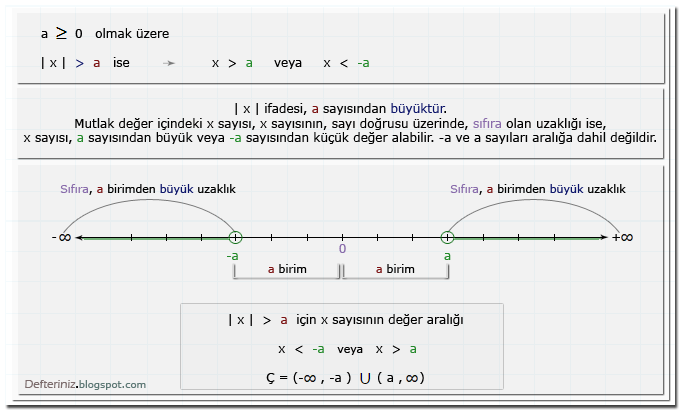
İfade Bir Sayıdan Büyük İse » | x | > a
a ≥ 0 olmak üzere
| x | > a ise
x > a veya x < -a
a sayısı, sıfıra eşit veya büyük olmak üzere → a ≥ 0
İfade a sayısından büyük ise → | x | > a
x sayısı, a sayısından büyük veya -a sayısından küçük değer alabilir
x > a veya x < -a → (-∞ , -a) ∪ (a , ∞)
a sayısından büyük sayılar, artı sonsuza giden tüm sayılardır. Artı sonsuz sayı, ∞ şeklinde gösterilir. -a sayısından küçük sayılar, eksi sonsuza giden tüm sayılardır. Eksi sonsuz sayı, -∞ şeklinde gösterilir.
Eşitsizlik büyüktür eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahil değildir. Büyük eşit eşitsizliği ile yazılmış olsaydı, -a ve a sayıları değer aralığına dahil olurdu.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olmadığı için,
parantezler içine, (-∞ , -a) ∪ (a , ∞) şeklinde yazılır ve sayı doğrusu üzerinde, içi boş çemberler (⚪) ile gösterilir. Eksi ve artı sonsuz sayıları, parantezler ile kapatılır.
İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
İfade bir sayıdan büyük ise » | x | > a:| x | > a ise
x > a veya x < -a
a sayısı, sıfıra eşit veya büyük olmak üzere → a ≥ 0
İfade a sayısından büyük ise → | x | > a
x sayısı, a sayısından büyük veya -a sayısından küçük değer alabilir
x > a veya x < -a → (-∞ , -a) ∪ (a , ∞)
a sayısından büyük sayılar, artı sonsuza giden tüm sayılardır. Artı sonsuz sayı, ∞ şeklinde gösterilir. -a sayısından küçük sayılar, eksi sonsuza giden tüm sayılardır. Eksi sonsuz sayı, -∞ şeklinde gösterilir.
Eşitsizlik büyüktür eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahil değildir. Büyük eşit eşitsizliği ile yazılmış olsaydı, -a ve a sayıları değer aralığına dahil olurdu.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olmadığı için,
parantezler içine, (-∞ , -a) ∪ (a , ∞) şeklinde yazılır ve sayı doğrusu üzerinde, içi boş çemberler (⚪) ile gösterilir. Eksi ve artı sonsuz sayıları, parantezler ile kapatılır.
İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Örnek:
İfade bir sayıdan büyük ise » | x | > 5:
İfade Bir Sayıdan Büyük Eşit İse » | x | ≥ a
a ≥ 0 olmak üzere
| x | ≥ a ise
x ≥ a veya x ≤ -a
İfade a sayısından büyük eşit ise → | x | ≥ a
x sayısı, a sayısına eşit veya büyük veya -a sayısına eşit veya küçük değer alabilir
x ≥ a veya x ≤ -a → (-∞ , -a] ∪ [a , ∞)
Eşitsizlik büyük eşit eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahildir.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olduğu için,
köşeli parantez ile, (-∞ , -a] ∪ [a , ∞) şeklinde yazılır ve sayı doğrusu üzerinde, içi dolu daireler (⚫) ile gösterilir. Eksi ve artı sonsuz sayıları, parantez ile kapatılır.
İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
İfade bir sayıdan büyük eşit ise » | x | ≥ a:| x | ≥ a ise
x ≥ a veya x ≤ -a
İfade a sayısından büyük eşit ise → | x | ≥ a
x sayısı, a sayısına eşit veya büyük veya -a sayısına eşit veya küçük değer alabilir
x ≥ a veya x ≤ -a → (-∞ , -a] ∪ [a , ∞)
Eşitsizlik büyük eşit eşitsizliği ile yazıldığından, değer aralığına -a ve a sayıları dahildir.
Değer aralığı (çözüm kümesi), -a ve a sayıları dahil olduğu için,
köşeli parantez ile, (-∞ , -a] ∪ [a , ∞) şeklinde yazılır ve sayı doğrusu üzerinde, içi dolu daireler (⚫) ile gösterilir. Eksi ve artı sonsuz sayıları, parantez ile kapatılır.
İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Örnek:
İfade bir sayıdan büyük eşit ise » | x | ≥ 5:
Örnek soru-4:
Mutlak değerli eşitsizlik » Örnek soru-4 » İfade bir sayıdan büyük eşit ise (kaynak: Supara 9. sınıf):
Örnek soru-5:
Mutlak değerli eşitsizlik » Örnek soru-5 » İki İfadenin Çözüm Kümesi Kesişimi (kaynak: Supara 9. sınıf):
Örnek soru-6:
Mutlak değerli eşitsizlik » Örnek soru-6 » İfade bir sayıdan büyük ise (kaynak: Supara 9. sınıf):
İfade Bir Sayıdan Büyük, Diğerinden Küçük İse » a < | x | < b
a ve b ∈ R⁺ olmak üzere
a < | x | < b ise
a < x < b veya -b < x < -a
a ve b pozitif gerçek sayı olmak üzere → a ve b ∈ R⁺
İfade a sayısından büyük, b sayısından küçük ise → a < | x | < b
x sayısı, a sayısından büyük, b sayısından küçük veya
-b sayısından büyük, -a sayısından küçük değer alabilir.
a < x < b veya -b < x < -a → (-b , -a) ∪ (a , b)
Eşitsizlik büyüktür ve küçüktür eşitsizlikleri ile yazıldığından, değer aralığına -b, -a, a ve b sayıları dahil değildir.
Değer aralığı (çözüm kümesi), -b, -a, a ve b sayıları dahil olmadığı için,
parantezler ile, (-b , -a) ∪ (a , b) şeklinde yazılır ve sayı doğrusu üzerinde, içi boş çemberler (⚪) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Mutlak değerli, a < | x | < b eşitsizliği, iki eşitsizlikten oluşur. Eşitsizliğin sol tarafında büyüktür ( a < | x | ) eşitsizliği, sağ tarafında küçüktür ( | x | < b ) eşitsizliği vardır.
İki eşitsizlik ayrı ayrı çözülebilir. İki eşitsizliğin çözüm kümelerinin kesişimi,
a < | x | < b eşitsizliğinin çözüm kümesidir.
Eşitsizlikler ayrı ayrı çözüldüğünde, 4 tane sayı aralığı olur.
Büyüktür eşitsizliğinin sayı aralıklarının birleşimi, büyüktür eşitsizliğinin çözüm kümesidir.
Küçüktür eşitsizliğinin sayı aralıklarının birleşimi, küçüktür eşitsizliğinin çözüm kümesidir.
İki çözüm kümesinin kesişimi, a < | x | < b eşitsizliğinin çözüm kümesidir.
İki sayı aralığının birleşimini bulmak, 4 sayı aralığının önce birleşimini sonra kesişimini bulmaktan daha kolay olacaktır.
İfade bir sayıdan büyük, diğerinden küçük ise » a < | x | < b:a < | x | < b ise
a < x < b veya -b < x < -a
a ve b pozitif gerçek sayı olmak üzere → a ve b ∈ R⁺
İfade a sayısından büyük, b sayısından küçük ise → a < | x | < b
x sayısı, a sayısından büyük, b sayısından küçük veya
-b sayısından büyük, -a sayısından küçük değer alabilir.
a < x < b veya -b < x < -a → (-b , -a) ∪ (a , b)
Eşitsizlik büyüktür ve küçüktür eşitsizlikleri ile yazıldığından, değer aralığına -b, -a, a ve b sayıları dahil değildir.
Değer aralığı (çözüm kümesi), -b, -a, a ve b sayıları dahil olmadığı için,
parantezler ile, (-b , -a) ∪ (a , b) şeklinde yazılır ve sayı doğrusu üzerinde, içi boş çemberler (⚪) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Mutlak değerli, a < | x | < b eşitsizliği, iki eşitsizlikten oluşur. Eşitsizliğin sol tarafında büyüktür ( a < | x | ) eşitsizliği, sağ tarafında küçüktür ( | x | < b ) eşitsizliği vardır.
İki eşitsizlik ayrı ayrı çözülebilir. İki eşitsizliğin çözüm kümelerinin kesişimi,
a < | x | < b eşitsizliğinin çözüm kümesidir.
Eşitsizlikler ayrı ayrı çözüldüğünde, 4 tane sayı aralığı olur.
Büyüktür eşitsizliğinin sayı aralıklarının birleşimi, büyüktür eşitsizliğinin çözüm kümesidir.
Küçüktür eşitsizliğinin sayı aralıklarının birleşimi, küçüktür eşitsizliğinin çözüm kümesidir.
İki çözüm kümesinin kesişimi, a < | x | < b eşitsizliğinin çözüm kümesidir.
İki sayı aralığının birleşimini bulmak, 4 sayı aralığının önce birleşimini sonra kesişimini bulmaktan daha kolay olacaktır.
Örnek:
İfade 2 sayısından büyük, 5 sayısından küçük ise » 2 < | x | < 5:
İfade Bir Sayıdan Büyük Eşit, Diğerinden Küçük İse » a ≤ | x | < b
a ve b ∈ R⁺ olmak üzere
a ≤ | x | < b ise
a ≤ x < b veya -b < x ≤ -a
İfade a sayısından büyük eşit, b sayısından küçük ise → a ≤ | x | < b
x sayısı, a sayısından büyük eşit, b sayısından küçük veya
-b sayısından büyük, -a sayısından küçük eşit değer alabilir.
a ≤ x < b veya -b < x ≤ -a → (-b , -a] ∪ [a , b)
Eşitsizlik büyük eşit ve küçüktür eşitsizlikleri ile yazıldığından, değer aralığına,
büyük eşit eşitsizliğinin değerleri a ve -a sayıları dahil,
küçüktür eşitsizliğinin değerleri b ve -b sayıları dahil değildir.
Değer aralığı (çözüm kümesi), a ve -a sayıları dahil olduğu için, a ve -a sayıları köşeli parantezler ile, b ve -b sayıları dahil olmadığı için, b ve -b sayıları parantezler ile,
(-b , -a] ∪ [a , b) şeklinde yazılır ve sayı doğrusu üzerinde, a ve -a sayıları içi dolu daireler (⚫), b ve -b sayıları içi boş çemberler (⚪) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
İfade bir sayıdan büyük eşit, diğerinden küçük ise » a ≤ | x | < b:a ≤ | x | < b ise
a ≤ x < b veya -b < x ≤ -a
İfade a sayısından büyük eşit, b sayısından küçük ise → a ≤ | x | < b
x sayısı, a sayısından büyük eşit, b sayısından küçük veya
-b sayısından büyük, -a sayısından küçük eşit değer alabilir.
a ≤ x < b veya -b < x ≤ -a → (-b , -a] ∪ [a , b)
Eşitsizlik büyük eşit ve küçüktür eşitsizlikleri ile yazıldığından, değer aralığına,
büyük eşit eşitsizliğinin değerleri a ve -a sayıları dahil,
küçüktür eşitsizliğinin değerleri b ve -b sayıları dahil değildir.
Değer aralığı (çözüm kümesi), a ve -a sayıları dahil olduğu için, a ve -a sayıları köşeli parantezler ile, b ve -b sayıları dahil olmadığı için, b ve -b sayıları parantezler ile,
(-b , -a] ∪ [a , b) şeklinde yazılır ve sayı doğrusu üzerinde, a ve -a sayıları içi dolu daireler (⚫), b ve -b sayıları içi boş çemberler (⚪) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Örnek:
İfade 2 sayısından büyük eşit, 5 sayısından küçük ise » 2 ≤ | x | < 5:
İfade Bir Sayıdan Büyük, Diğerinden Küçük Eşit İse » a < | x | ≤ b
a ve b ∈ R⁺ olmak üzere
a < | x | ≤ b ise
a < x ≤ b veya -b ≤ x < -a
İfade a sayısından büyük, b sayısından küçük eşit ise → a < | x | ≤ b
x sayısı, a sayısından büyük, b sayısından küçük eşit veya
-b sayısından büyük eşit, -a sayısından küçük değer alabilir.
a < x ≤ b veya -b ≤ x < -a → [-b , -a) ∪ (a , b]
Eşitsizlik büyüktür ve küçük eşit eşitsizlikleri ile yazıldığından, değer aralığına,
büyüktür eşitsizliğinin değerleri a ve -a sayıları dahil değil,
küçük eşit eşitsizliğinin değerleri b ve -b sayıları dahildir.
Değer aralığı (çözüm kümesi), a ve -a sayıları dahil olmadığı için, a ve -a sayıları parantezler ile, b ve -b sayıları dahil olduğu için, b ve -b sayıları köşeli parantezler ile,
[-b , -a) ∪ (a , b] şeklinde yazılır ve sayı doğrusu üzerinde, a ve -a sayıları içi boş çemberler (⚪), b ve -b sayıları içi dolu daireler (⚫) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
İfade bir sayıdan büyük, diğerinden küçük eşit ise » a < | x | ≤ b:a < | x | ≤ b ise
a < x ≤ b veya -b ≤ x < -a
İfade a sayısından büyük, b sayısından küçük eşit ise → a < | x | ≤ b
x sayısı, a sayısından büyük, b sayısından küçük eşit veya
-b sayısından büyük eşit, -a sayısından küçük değer alabilir.
a < x ≤ b veya -b ≤ x < -a → [-b , -a) ∪ (a , b]
Eşitsizlik büyüktür ve küçük eşit eşitsizlikleri ile yazıldığından, değer aralığına,
büyüktür eşitsizliğinin değerleri a ve -a sayıları dahil değil,
küçük eşit eşitsizliğinin değerleri b ve -b sayıları dahildir.
Değer aralığı (çözüm kümesi), a ve -a sayıları dahil olmadığı için, a ve -a sayıları parantezler ile, b ve -b sayıları dahil olduğu için, b ve -b sayıları köşeli parantezler ile,
[-b , -a) ∪ (a , b] şeklinde yazılır ve sayı doğrusu üzerinde, a ve -a sayıları içi boş çemberler (⚪), b ve -b sayıları içi dolu daireler (⚫) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Örnek:
İfade 2 sayısından büyük, 5 sayısından küçük eşit ise » 2 < | x | ≤ 5:
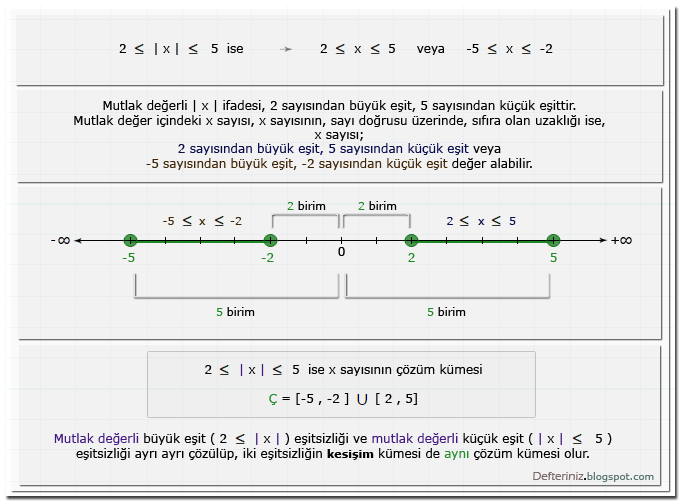
İfade Bir Sayıdan Büyük Eşit, Diğerinden Küçük Eşit İse » a ≤ | x | ≤ b
a ve b ∈ R⁺ olmak üzere
a ≤ | x | ≤ b ise
a ≤ x ≤ b veya -b ≤ x ≤ -a
İfade a sayısından büyük eşit, b sayısından küçük eşit ise → a ≤ | x | ≤ b
x sayısı, a sayısından büyük eşit, b sayısından küçük eşit veya
-b sayısından büyük eşit, -a sayısından küçük eşit değer alabilir.
a ≤ x ≤ b veya -b ≤ x ≤ -a → [-b , -a] ∪ [a , b]
Eşitsizlik büyük eşit ve küçük eşit eşitsizlikleri ile yazıldığından, değer aralığına,
a , -a , b ve -b sayıları dahildir.
Değer aralığı (çözüm kümesi), a , -a , b ve -b sayıları dahil olduğu için köşeli parantezler ile, [-b , -a] ∪ [a , b] şeklinde yazılır ve sayı doğrusu üzerinde, içi dolu daireler (⚫) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
İfade bir sayıdan büyük eşit, diğerinden küçük eşit ise » a ≤ | x | ≤ b:a ≤ | x | ≤ b ise
a ≤ x ≤ b veya -b ≤ x ≤ -a
İfade a sayısından büyük eşit, b sayısından küçük eşit ise → a ≤ | x | ≤ b
x sayısı, a sayısından büyük eşit, b sayısından küçük eşit veya
-b sayısından büyük eşit, -a sayısından küçük eşit değer alabilir.
a ≤ x ≤ b veya -b ≤ x ≤ -a → [-b , -a] ∪ [a , b]
Eşitsizlik büyük eşit ve küçük eşit eşitsizlikleri ile yazıldığından, değer aralığına,
a , -a , b ve -b sayıları dahildir.
Değer aralığı (çözüm kümesi), a , -a , b ve -b sayıları dahil olduğu için köşeli parantezler ile, [-b , -a] ∪ [a , b] şeklinde yazılır ve sayı doğrusu üzerinde, içi dolu daireler (⚫) ile gösterilir. İki sayı aralığının birleşimi, eşitsizliğin çözüm kümesidir.
Örnek:
İfade 2 sayısından büyük eşit, 5 sayısından küçük eşit ise » 2 ≤ | x | ≤ 5:
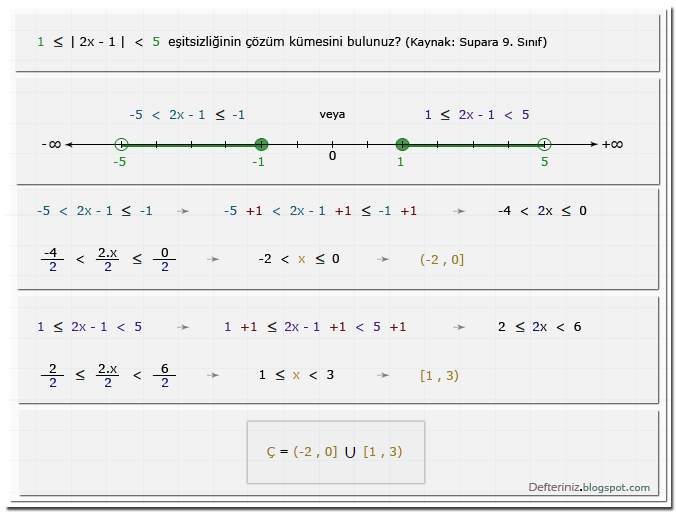
Örnek soru-7:
Mutlak değerli eşitsizlik » Örnek soru-7 » İfade bir sayıdan büyük eşit diğerinden küçük ise (kaynak: Supara 9. sınıf):
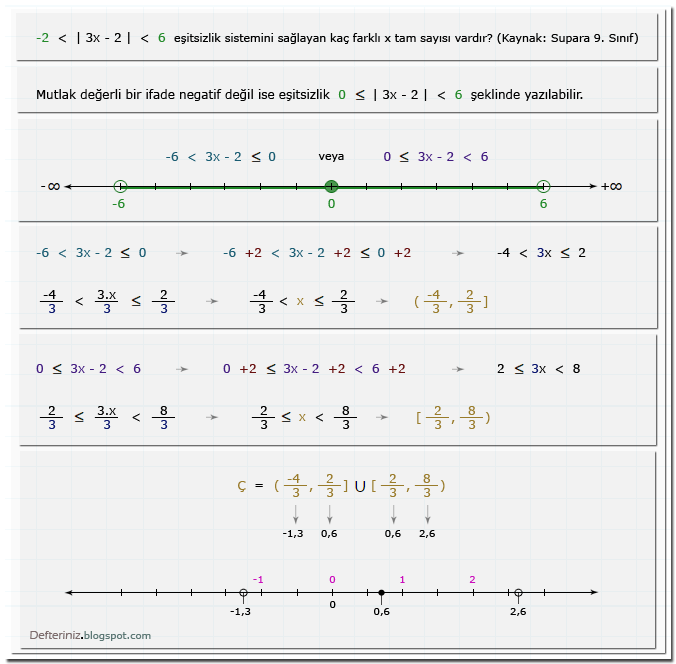
Örnek soru-8:
Mutlak değerli eşitsizlik » Örnek soru-8 » İfade bir sayıdan büyük eşit diğerinden küçük ise (kaynak: Supara 9. sınıf):
İki Tarafında Mutlak Değerli İfade Olan Eşitsizlikler
İki tarafında da mutlak değerli ifadeler olan bir eşitsizlik çözümünde:- Mutlak değer içindeki ifadelerin karesi (2. kuvveti) alınır
- Eşitsizlik sembolü aynen yazılır
Eşitsizlik küçük eşit ise:
| x | ≤ | y | ise x² ≤ y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden küçük eşit ise → | x | ≤ | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden küçük eşittir → x² ≤ y²
| x | ≤ | y | ise x² ≤ y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden küçük eşit ise → | x | ≤ | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden küçük eşittir → x² ≤ y²
Eşitsizlik küçüktür ise:
| x | < | y | ise x² < y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden küçük ise → | x | < | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden küçüktür → x² < y²
| x | < | y | ise x² < y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden küçük ise → | x | < | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden küçüktür → x² < y²
Eşitsizlik büyük eşit ise:
| x | ≥ | y | ise x² ≥ y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden büyük eşit ise → | x | ≥ | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden büyük eşittir → x² ≥ y²
| x | ≥ | y | ise x² ≥ y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden büyük eşit ise → | x | ≥ | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden büyük eşittir → x² ≥ y²
Eşitsizlik büyüktür ise:
| x | >| y | ise x² > y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden büyük ise → | x | > | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden büyüktür → x² > y²
İfade, diğer ifadeden küçük eşit ise » | x | ≤ | y |:| x | >| y | ise x² > y²
Mutlak değerli | x | ifadesi, mutlak değerli | y | ifadesinden büyük ise → | x | > | y |
Mutlak değer içindeki x sayısının karesi, mutlak değer içindeki y sayısının karesinden büyüktür → x² > y²
Örnek soru-9:
Mutlak değerli eşitsizlik » Örnek soru-9 » İki tarafında mutlak değerli ifade olan eşitsizlikler (kaynak: Supara 9. sınıf):
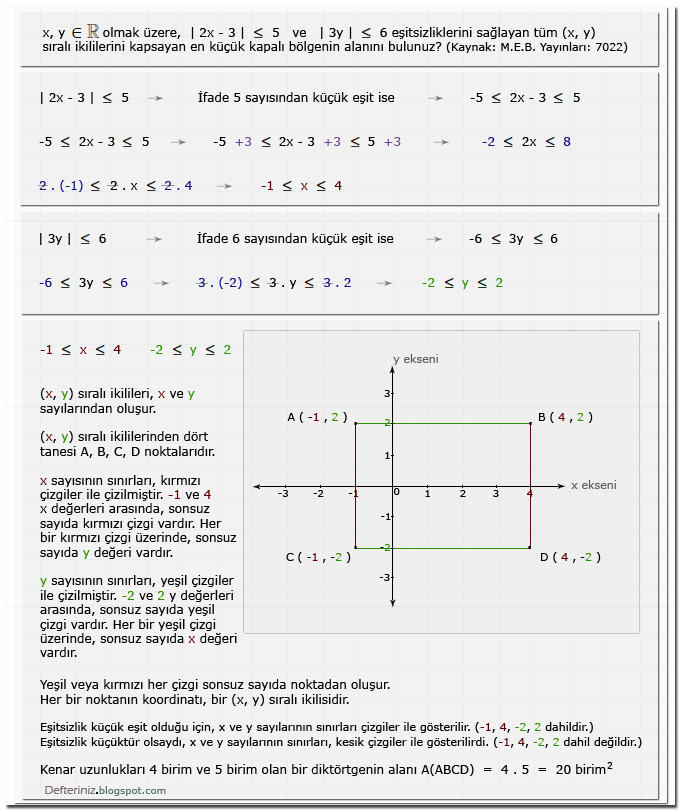
(x, y) Sıralı İkililerinin Analitik (Koordinat) Düzlemde Gösterilmesi
Örnek soru-10:Mutlak değerli eşitsizlik » Örnek soru-10 » (x, y) Sıralı İkilileri » Analitik (Koordinat) Düzlem (kaynak: M.E.B. Yayınları: 7022):



















Yorumlar
Yorum Gönder