Şu an 3. Bölüm görüntüleniyor...
Örnek:
|x| = 2 denkleminin çözüm kümesi nedir?
Çözüm:
Mutlak değer içindeki x sayısı, pozitif veya negatif olabilir.
Mutlak değerli denklem » Örnek soru-1 » İfade bir sayıya eşit ise (kaynak: Supara 9. sınıf):
Örnek:
|x| = -3 denkleminin çözüm kümesi nedir?
Çözüm:
Mutlak değerli denklem » Çözüm kümesi boş küme:
Örnek soru-2:
Mutlak değerli denklem » Örnek soru-2 » İfade sıfırdan küçük ise (boş küme) (kaynak: Supara 9. sınıf):
Örnek soru-3:
Mutlak değerli denklem » Örnek soru-3 » Özellikler (kaynak: Supara 9. sınıf):
Mutlak değerli denklem » Örnek soru-4 » Özellikler (kaynak: Supara 9. sınıf):
Mutlak değerli denklem » Örnek soru-5 » |x| = y ise (kaynak: Supara 9. sınıf):
Mutlak değerli denklem » | x | = | y |:
Örnek soru-6:
Mutlak değerli denklem » Örnek soru-6 » |x| = |y| ise (kaynak: Supara 9. sınıf):
Mutlak değerli denklem örnek A » | x | ± a = | y | (Kaynak: M.E.B. Yayınları - 7022):
Mutlak değerli denklem örnek B » | x | ± a = | y | (Kaynak: M.E.B. Yayınları - 7022):
Mutlak değerli denklem » |x| + |y| = 0:
Örnek soru-7:
Mutlak değerli denklem » Örnek soru-7 » |x| + |y| = 0 ise (kaynak: Supara 9. sınıf):
Örnek soru-8:
Mutlak değerli denklem » Örnek soru-8 » | x . y | = | a . y | ise (kaynak: Supara 9. sınıf):
Mutlak değerli denklem » Örnek soru-9 » (x, y) Sıralı İkilileri » Analitik (Koordinat) Düzlem (kaynak: M.E.B. Yayınları: 7022):
Mutlak Değerli Denklemler
Mutlak değerli ifade bulunan denklemlere, mutlak değerli denklem denir.İfade Bir Sayıya Eşit ise » | x | = a
a ≥ 0 olmak üzere
| x | = a ise
x = a veya x = -a olabilir.
Bilinmeyeni x olan mutlak değerli bir ifade, a sayısına eşit ise, x bilinmeyeni a veya -a olabilir. Denklemin eşit olduğu a sayısı sıfıra eşit veya sıfırdan büyük bir sayıdır. Denklemin kökleri olan a ve -a sayıları, pozitif, negatif veya sıfır olabilir.| x | = a ise
x = a veya x = -a olabilir.
Örnek:
|x| = 2 denkleminin çözüm kümesi nedir?
Çözüm:
Mutlak değer içindeki x sayısı, pozitif veya negatif olabilir.
x sayısı pozitif ise dışarı aynen çıkar.
x = 2
x = 2
x sayısı negatif ise dışarı çıkarken (-) ile çarpılır.
-x = 2
-x = 2 eşitliğinin her iki tarafı (-) ile çarpılır ise, x sayısı pozitif olur. Denklemin kökleri bulunurken x sayısının işareti pozitif olmalıdır.
(-).(-x) = (-).2
+x = -2
x = -2
-x = 2
-x = 2 eşitliğinin her iki tarafı (-) ile çarpılır ise, x sayısı pozitif olur. Denklemin kökleri bulunurken x sayısının işareti pozitif olmalıdır.
(-).(-x) = (-).2
+x = -2
x = -2
|x| = 2 denkleminin çözüm kümesi → Ç = {2 , -2} dir.
|x| = 2 denklemi çözülürken, x negatif ise, x in çarpıldığı (-) işareti, ifadenin eşit olduğu 2 sayısına verilerek, x değerleri
x = 2
x = -2
şeklinde yazılır.
Örnek soru-1:x = 2
x = -2
şeklinde yazılır.
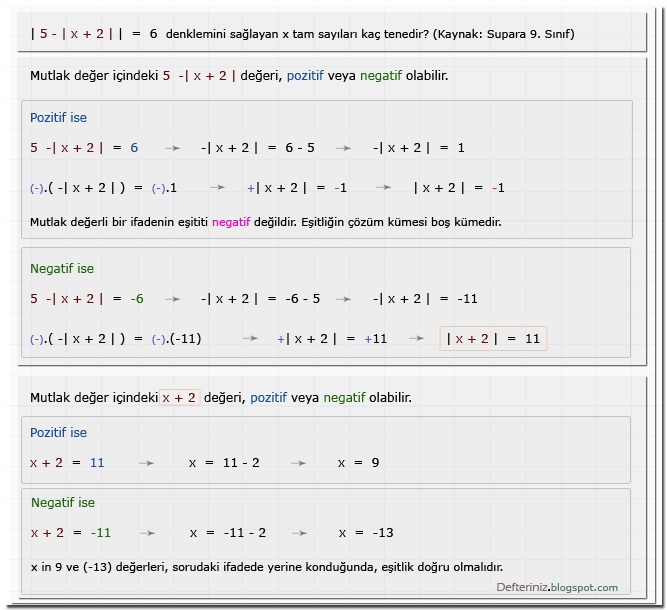
Mutlak değerli denklem » Örnek soru-1 » İfade bir sayıya eşit ise (kaynak: Supara 9. sınıf):
İfadenin eşiti sıfırdan küçük ise » | x | = a (a < 0) (Boş Küme)
a < 0 olmak üzere
| x | = a ise
Ç = ∅
Bilinmeyeni x olan mutlak değerli bir ifadenin eşiti, sıfırdan küçük ise, denklemin çözüm kümesi boş kümedir.| x | = a ise
Ç = ∅
Örnek:
|x| = -3 denkleminin çözüm kümesi nedir?
Çözüm:
Mutlak değerli bir ifadenin değeri negatif değildir.
Denklemin çözüm kümesi boş kümedir.
Ç = ∅
Örnek:Denklemin çözüm kümesi boş kümedir.
Ç = ∅
Mutlak değerli denklem » Çözüm kümesi boş küme:
Örnek soru-2:
Mutlak değerli denklem » Örnek soru-2 » İfade sıfırdan küçük ise (boş küme) (kaynak: Supara 9. sınıf):
Örnek soru-3:
Mutlak değerli denklem » Örnek soru-3 » Özellikler (kaynak: Supara 9. sınıf):
Not:
Denklemin bilinmeyeni x ise, özellikler ile denklemdeki ifadeler, |x|, |x + 1|, |2x + 1| gibi ifadelere benzetilebilir. Öncelikle tüm ifadeler; |x|, |x + 1|, |2x + 1| gibi ifadelere benzetebiliyor ise, denklem bu yolla çözülmeye çalışılabilir.
Aynı ifadeye benzetilemeyen denklemler diğer çözüm yolları ile çözülebilir.
Örnek soru-4:Denklemin bilinmeyeni x ise, özellikler ile denklemdeki ifadeler, |x|, |x + 1|, |2x + 1| gibi ifadelere benzetilebilir. Öncelikle tüm ifadeler; |x|, |x + 1|, |2x + 1| gibi ifadelere benzetebiliyor ise, denklem bu yolla çözülmeye çalışılabilir.
Aynı ifadeye benzetilemeyen denklemler diğer çözüm yolları ile çözülebilir.
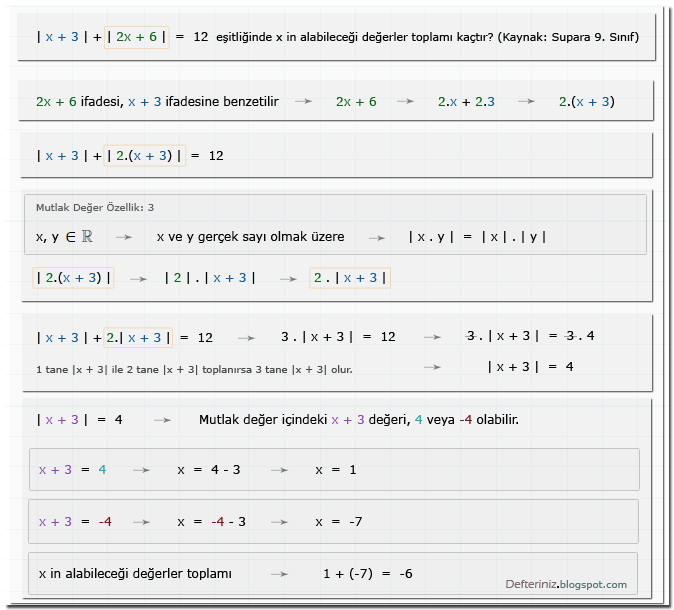
Mutlak değerli denklem » Örnek soru-4 » Özellikler (kaynak: Supara 9. sınıf):
Mutlak Değerli İfade, Bilinmeyenli İfadeye Eşit ise » | x | = y
| x | = y ise
x = y veya x = -y olabilir.
x = y veya x = -y olabilir.
Bilinmeyeni x olan mutlak değerli bir ifade, y değerine eşit ise, x bilinmeyeni y veya -y olabilir. İfadenin eşit olduğu y değeri, başka bir ifadeye eşit olabilir. Örneğin; (x + 1) , (2x + 3) gibi...
|x + 2| = 3x + 1 şeklinde kurulan denklemlerdir. Eşitliğin bir tarafında mutlak değerli ifade, diğer tarafında bilinmeyenli ifade bulunan denklemlerdir.
|x + 2| = 3x + 1 şeklinde kurulan denklemlerdir. Eşitliğin bir tarafında mutlak değerli ifade, diğer tarafında bilinmeyenli ifade bulunan denklemlerdir.
|x + 2| = 3x + 1 denklemi için:
Mutlak değer içindeki x + 2 değeri pozitif veya negatif olabilir.
x + 2 → pozitif ise, aynen dışarı çıkar → x + 2 = 3x + 1
x + 2 → negatif ise, (-) ile çarpılır. → -(x + 2) = 3x + 1
(x + 2) ifadesinin (-) işareti, eşitliğin diğer tarafına verilerek, eşitlik, x + 2 = -(3x + 1) şeklinde yazılabilir.
Mutlak değer içindeki x + 2 değeri pozitif veya negatif olabilir.
x + 2 → pozitif ise, aynen dışarı çıkar → x + 2 = 3x + 1
x + 2 → negatif ise, (-) ile çarpılır. → -(x + 2) = 3x + 1
(x + 2) ifadesinin (-) işareti, eşitliğin diğer tarafına verilerek, eşitlik, x + 2 = -(3x + 1) şeklinde yazılabilir.
Mutlak değerli ifadenin bir sayıya eşit olduğu denklemlerde olduğu gibi, iki eşitlik yazılır.
x + 2 = 3x + 1
x + 2 = -(3x + 1)
x + 2 = 3x + 1
x + 2 = -(3x + 1)
İki eşitlik için, bulunan x değerleri, mutlak değerin eşiti olan 3x + 1 değerini, pozitif yapmalıdır. Bulunan x değerleri, 3x + 1 ifadesinde yerine konur.
3x + 1 ifadesini pozitif yapan x değeri, denklemin köküdür.
Mutlak değerli bir ifadenin eşiti negatif değildir. 3x + 1 ifadesini negatif yapan x değeri, denklemin kökü değildir.
Örnek soru-5:3x + 1 ifadesini pozitif yapan x değeri, denklemin köküdür.
Mutlak değerli bir ifadenin eşiti negatif değildir. 3x + 1 ifadesini negatif yapan x değeri, denklemin kökü değildir.
Mutlak değerli denklem » Örnek soru-5 » |x| = y ise (kaynak: Supara 9. sınıf):
Mutlak Değerli İfade, Mutlak Değerli İfadeye Eşit ise » | x | = | y |
| x | = | y | ise
x = y veya x = -y olabilir.
x = y veya x = -y olabilir.
Bilinmeyeni x olan mutlak değerli bir ifade, mutlak değerli | y | ifadesine eşit ise, x bilinmeyeni y veya -y olabilir.
|x + 2| = |2x + 5| şeklinde kurulan denklemlerdir. Eşitliğin bir tarafında mutlak değerli ifade, diğer tarafında yine mutlak değerli ifade bulunan denklemlerdir.
|x + 2| = |2x + 5| şeklinde kurulan denklemlerdir. Eşitliğin bir tarafında mutlak değerli ifade, diğer tarafında yine mutlak değerli ifade bulunan denklemlerdir.
Denklemin çözümü için iki eşitlik yazılır.
x + 2 = 2x + 5
x + 2 = -(2x + 5)
Örnek:x + 2 = 2x + 5
x + 2 = -(2x + 5)
Mutlak değerli denklem » | x | = | y |:
Örnek soru-6:
Mutlak değerli denklem » Örnek soru-6 » |x| = |y| ise (kaynak: Supara 9. sınıf):
Mutlak Değer Tanımı (Kritik Nokta) ile Çözülen Denklemler
| x | ± a = | y |
| x | ± | y | = a
şeklinde olan denklemlerdir. x ve y mutlak değer içindeki bilinmeyenli ifadeler, a gerçek sayıdır (a ≠ 0).
Özellikler ile denklemdeki ifadeler, |x|, |x + 1|, |2x + 1| gibi aynı ifadelere benzetilemiyor ise, denklem, mutlak değer tanımı (kritik nokta) ile çözülür.
|3x + 6| - 2 = |x - 1| şeklinde kurulan denklemlerdir.
Örnek:| x | ± | y | = a
şeklinde olan denklemlerdir. x ve y mutlak değer içindeki bilinmeyenli ifadeler, a gerçek sayıdır (a ≠ 0).
Özellikler ile denklemdeki ifadeler, |x|, |x + 1|, |2x + 1| gibi aynı ifadelere benzetilemiyor ise, denklem, mutlak değer tanımı (kritik nokta) ile çözülür.
|3x + 6| - 2 = |x - 1| şeklinde kurulan denklemlerdir.
Mutlak değerli denklem örnek A » | x | ± a = | y | (Kaynak: M.E.B. Yayınları - 7022):
Mutlak değerli denklem örnek B » | x | ± a = | y | (Kaynak: M.E.B. Yayınları - 7022):
Mutlak Değerli İfadelerin Toplamı Sıfıra Eşit İse » |x| + |y| = 0
| x | + | y | = 0 ise
x = 0 ve y = 0 dır.
x = 0 ve y = 0 dır.
Mutlak değerli bir ifadenin değeri sıfır veya sıfırdan büyük olabilir.
Değeri pozitif olan, iki mutlak değerli ifadenin toplamı sıfırdan büyüktür.
Değeri sıfır olan ve değeri pozitif olan iki ifadenin toplamı sıfırdan büyüktür.
Mutlak değerli iki ifadenin toplamı sıfır ise, mutlak değerli ifadeler sıfıra eşit olmalıdır.
|2x + 6| + |y - 2| = 0 şeklinde kurulan denklemlerdir. Mutlak değerli ifade ile mutlak değerli ifadenin toplamı sıfıra eşittir.
Değeri pozitif olan, iki mutlak değerli ifadenin toplamı sıfırdan büyüktür.
Değeri sıfır olan ve değeri pozitif olan iki ifadenin toplamı sıfırdan büyüktür.
Mutlak değerli iki ifadenin toplamı sıfır ise, mutlak değerli ifadeler sıfıra eşit olmalıdır.
|2x + 6| + |y - 2| = 0 şeklinde kurulan denklemlerdir. Mutlak değerli ifade ile mutlak değerli ifadenin toplamı sıfıra eşittir.
Denklemin çözümü için iki eşitlik yazılır.
2x + 6 = 0
y - 2 = 0
Örnek:2x + 6 = 0
y - 2 = 0
Mutlak değerli denklem » |x| + |y| = 0:
Örnek soru-7:
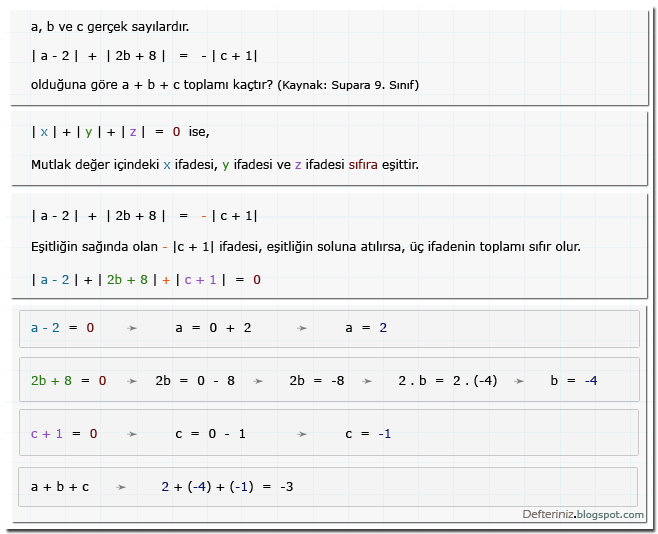
Mutlak değerli denklem » Örnek soru-7 » |x| + |y| = 0 ise (kaynak: Supara 9. sınıf):
Çarpanlarına Ayrılan İfadeler » | x . y | = | a . y |
x ve y mutlak değer içindeki, bilinmeyenli iki ifade ve a gerçek sayı olmak üzere (a ≠ 0)- | x . y | = | a . y | ise,
- | x . y | ifadesi, özellikler ile → | x | . | y | şeklinde yazılır.
- | a . y | ifadesi, özellikler ile → | a | . | y | şeklinde yazılır.
- Yeni eşitlik → | x | . | y | = | a | . | y |
| y | ifadeleri sadeleşir ise, y değeri bulunamayacağı için, sadeleşme işlemi yapılmamalıdır. - | a | . | y | ifadesi eşitliğin soluna atılır. → | x | . | y | - | a | . | y | = 0
- Eşitlik, | y | parantezine alınır. → | y |.( | x | - | a | ) = 0
- İki eşitlik yazılır. → | y | = 0 ve | x | - | a | = 0
- | (x + 2) . (x - 3) | = | 2.(x - 3) | ise,
- | (x + 2) . (x - 3) | ifadesi, özellikler ile → | x + 2 | . | x - 3 | şeklinde yazılır.
- | 2.(x - 3) | ifadesi, özellikler ile → | 2 | . | x - 3 | → 2 . | x - 3 | şeklinde yazılır.
- Yeni eşitlik → | x + 2 | . | x - 3 | = 2 . | x - 3 |
| x - 3 | ifadeleri sadeleşir ise, | x - 3 | ifadesindeki x değeri bulunamayacağı için, sadeleşme işlemi yapılmamalıdır. - 2 . | x - 3 | ifadesi eşitliğin soluna atılır. → | x + 2 | . | x - 3 | - 2 . | x - 3 | = 0
- Eşitlik, | x - 3 | parantezine alınır. → | x - 3 |.( | x + 2 | - 2 ) = 0
- İki eşitlik yazılır. → | x - 3 | = 0 ve | x + 2 | - 2 = 0
- | (x + 2) . (x - 3) | = | (2x - 3) . (x - 3) | ise,
- | (x + 2) . (x - 3) | ifadesi, özellikler ile → | x + 2 | . | x - 3 | şeklinde yazılır.
- | (2x - 3) . (x - 3) | ifadesi, özellikler ile → | 2x - 3 | . | x - 3 | şeklinde yazılır.
- Yeni eşitlik → | x + 2 | . | x - 3 | = | 2x - 3 | . | x - 3 |
| x - 3 | ifadeleri sadeleşir ise, | x - 3 | ifadesindeki x değeri bulunamayacağı için, sadeleşme işlemi yapılmamalıdır. - | 2x - 3 | . | x - 3 | ifadesi eşitliğin soluna atılır. → | x + 2 | . | x - 3 | - | 2x - 3 | . | x - 3 | = 0
- Eşitlik, | x - 3 | parantezine alınır. → | x - 3 |.( | x + 2 | - | 2x - 3 | ) = 0
- İki eşitlik yazılır.
| x - 3 | = 0 ve
| x + 2 | - | 2x - 3 | = 0 → | x + 2 | = | 2x - 3 |
Mutlak değerli denklem » Örnek soru-8 » | x . y | = | a . y | ise (kaynak: Supara 9. sınıf):
(x, y) Sıralı İkililerinin Analitik (Koordinat) Düzlemde Gösterilmesi
Örnek soru-9:Mutlak değerli denklem » Örnek soru-9 » (x, y) Sıralı İkilileri » Analitik (Koordinat) Düzlem (kaynak: M.E.B. Yayınları: 7022):











Yorumlar
Yorum Gönder