Şu an 2. Bölüm görüntüleniyor...
Örnek soru-1:
Mutlak değer özellik » Örnek soru-1 » İki sayının farkı (kaynak: Supara 9. sınıf):
Örnek:
Mutlak değer özellik » Örnek » İki sayının çarpımı:
Örnek soru-2:
Mutlak değer özellik » Örnek soru-2 » İki sayının çarpımı (kaynak: Supara 9. sınıf):
Örnek:
Mutlak değer özellik » Örnek » Kesirli ifadenin mutlak değeri:
Örnek soru-3:
Mutlak değer özellik » Örnek soru-3 » İfadenin alabileceği en büyük değer (kaynak: Supara 9. sınıf):
Mutlak Değerin Özellikleri
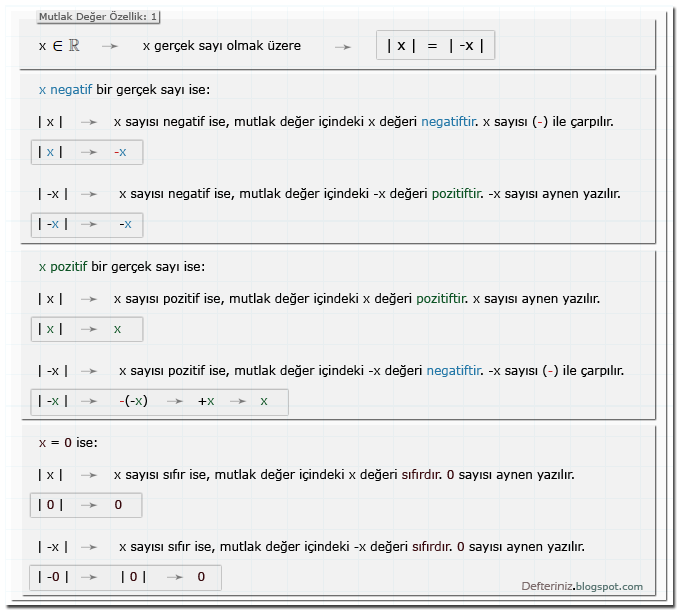
Özellik-1 » | x | = | -x |
x ∈ R → x gerçek sayı olmak üzere → | x | = | -x |
Mutlak değer » özellik-1 » | x | = | -x |:
Negatif (-3) sayısı için:
| -3 | → (-3) sayısı negatif ise, mutlak değer içindeki (-3) sayısı negatiftir. (-3) sayısı, (-) ile çarpılır.
| -3 | → -(-3) → +3 → 3
| -(-3) | → (-3) sayısı negatif ise, mutlak değer içindeki -(-3) sayısı pozitiftir. -(-3) sayısı, aynen yazılır.
| -(-3) | → -(-3) → +3 → 3
| -3 | = | -(-3) |
3 = 3
| -3 | → (-3) sayısı negatif ise, mutlak değer içindeki (-3) sayısı negatiftir. (-3) sayısı, (-) ile çarpılır.
| -3 | → -(-3) → +3 → 3
| -(-3) | → (-3) sayısı negatif ise, mutlak değer içindeki -(-3) sayısı pozitiftir. -(-3) sayısı, aynen yazılır.
| -(-3) | → -(-3) → +3 → 3
| -3 | = | -(-3) |
3 = 3
Pozitif 3 sayısı için:
| 3 | → 3 sayısı pozitif ise, mutlak değer içindeki 3 sayısı pozitiftir. 3 sayısı, aynen yazılır.
| 3 | → 3
| -3 | → 3 sayısı pozitif ise, mutlak değer içindeki (-3) sayısı negatiftir. (-3) sayısı, (-) ile çarpılır.
| -3 | → -(-3) → +3 → 3
| 3 | = | -3 |
3 = 3
| 3 | → 3 sayısı pozitif ise, mutlak değer içindeki 3 sayısı pozitiftir. 3 sayısı, aynen yazılır.
| 3 | → 3
| -3 | → 3 sayısı pozitif ise, mutlak değer içindeki (-3) sayısı negatiftir. (-3) sayısı, (-) ile çarpılır.
| -3 | → -(-3) → +3 → 3
| 3 | = | -3 |
3 = 3
İşareti olmayan sıfır (0) sayısı için:
| 0 | → Mutlak değer içindeki 0 sayısı, aynen yazılır.
| 0 | → 0
| -0 | → Mutlak değer içindeki (-0) sayısı, sıfırdır. 0 sayısı, aynen yazılır.
| -0 | → | 0 | → 0
| 0 | = | -0|
0 = 0
| 0 | → Mutlak değer içindeki 0 sayısı, aynen yazılır.
| 0 | → 0
| -0 | → Mutlak değer içindeki (-0) sayısı, sıfırdır. 0 sayısı, aynen yazılır.
| -0 | → | 0 | → 0
| 0 | = | -0|
0 = 0
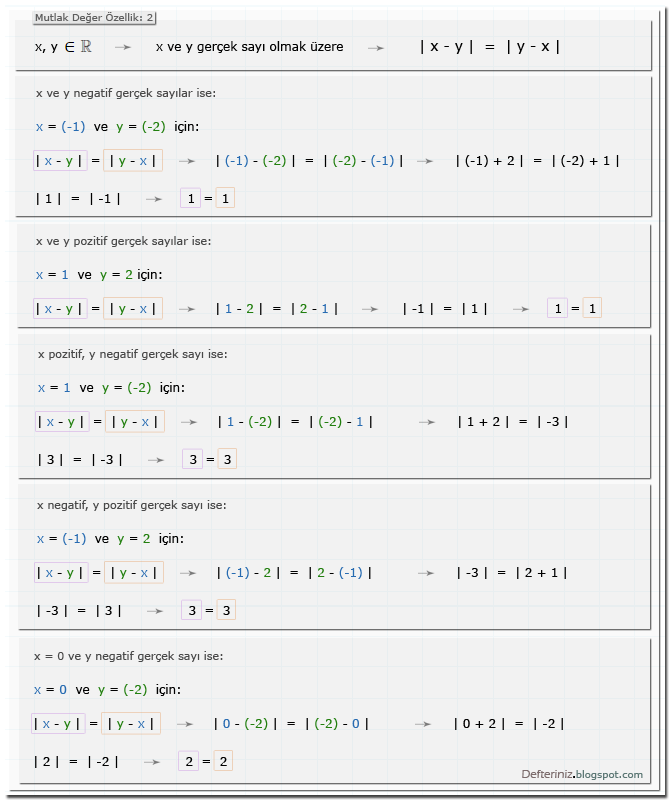
Özellik-2 » | x - y | = | y - x |
x, y ∈ R → x ve y gerçek sayılar olmak üzere → | x - y | = | y - x |
Mutlak değer » özellik-2 » | x - y | = | y - x |:Örnek soru-1:
Mutlak değer özellik » Örnek soru-1 » İki sayının farkı (kaynak: Supara 9. sınıf):
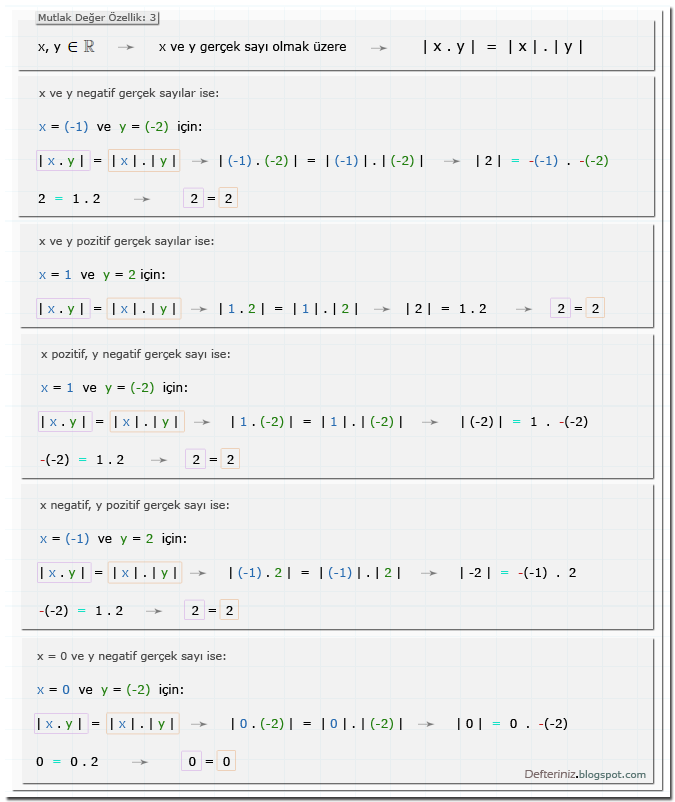
Özellik-3 » | x . y | = | x | . | y |
x, y ∈ R → x ve y gerçek sayılar olmak üzere → | x . y | = | x | . | y |
Mutlak değer » özellik-3 » | x . y | = | x | . | y |:Örnek:
Mutlak değer özellik » Örnek » İki sayının çarpımı:
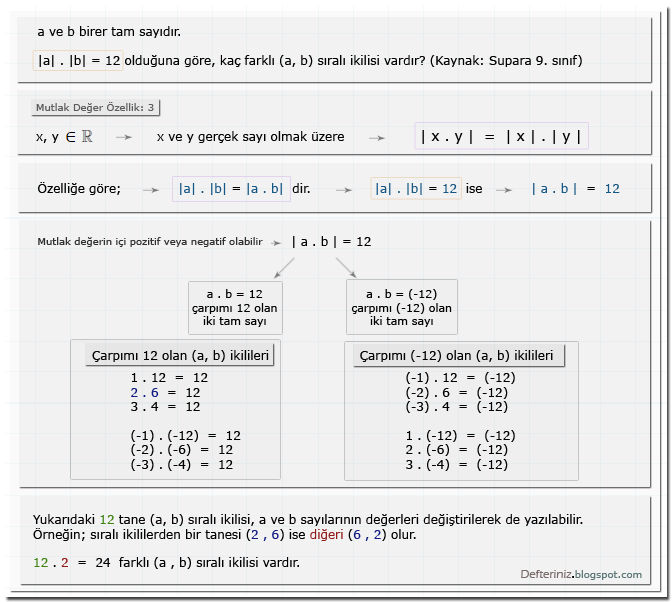
Örnek soru-2:
Mutlak değer özellik » Örnek soru-2 » İki sayının çarpımı (kaynak: Supara 9. sınıf):
Özellik-4 » | x / y | = | x | / | y |
x, y ∈ R → x ve y gerçek sayılar ve y ≠ 0 olmak üzere → | x / y | = | x | / | y |
Mutlak değer » özellik-4 » | x / y | = | x | / | y |:Örnek:
Mutlak değer özellik » Örnek » Kesirli ifadenin mutlak değeri:
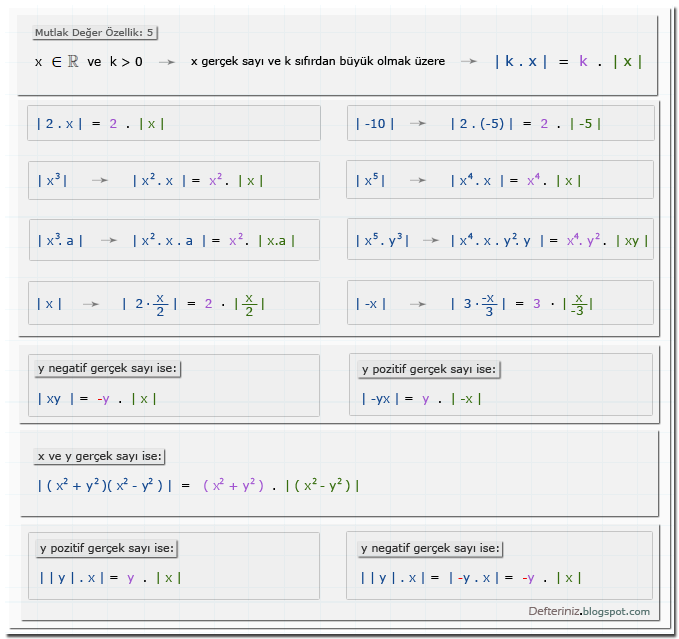
Özellik-5 » | k . x | = k . | x |
x ∈ R ve k > 0 → x gerçek sayı ve k sıfırdan büyük olmak üzere → | k . x | = k . | x |
Mutlak değer » özellik-5 » | k . x | = k . | x |:Özellik-6 » | xⁿ | = | x |ⁿ
x ∈ R → x gerçek sayı olmak üzere → | xⁿ | = | x |ⁿ
Mutlak değer » özellik-6 » | xⁿ | = | x |ⁿ:Özellik-7 » | x |²ⁿ = x²ⁿ
x ∈ R ve n ∈ Z → x gerçek sayı ve n tam sayı olmak üzere → | x |²ⁿ = x²ⁿ
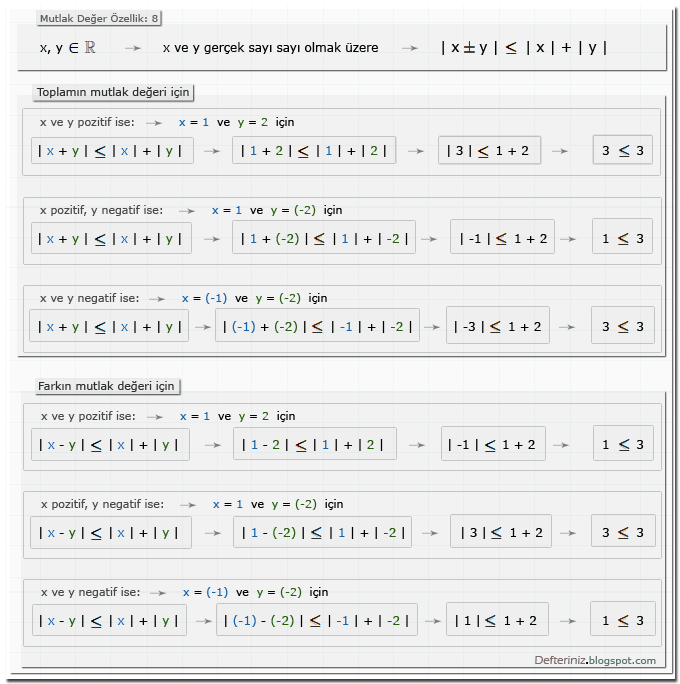
Mutlak değer » özellik-7 » | x |²ⁿ = x²ⁿ:Özellik-8 » | x ± y | ≤ | x | + | y |
x, y ∈ R → x ve y gerçek sayı olmak üzere → | x ± y | ≤ | x | + | y |
İki sayının toplamının veya farkının mutlak değeri, sayıların mutlak değerleri toplamından küçük veya eşittir.
Mutlak değer » özellik-8 » | x ± y | ≤ | x | + | y |:İki sayının toplamının veya farkının mutlak değeri, sayıların mutlak değerleri toplamından küçük veya eşittir.
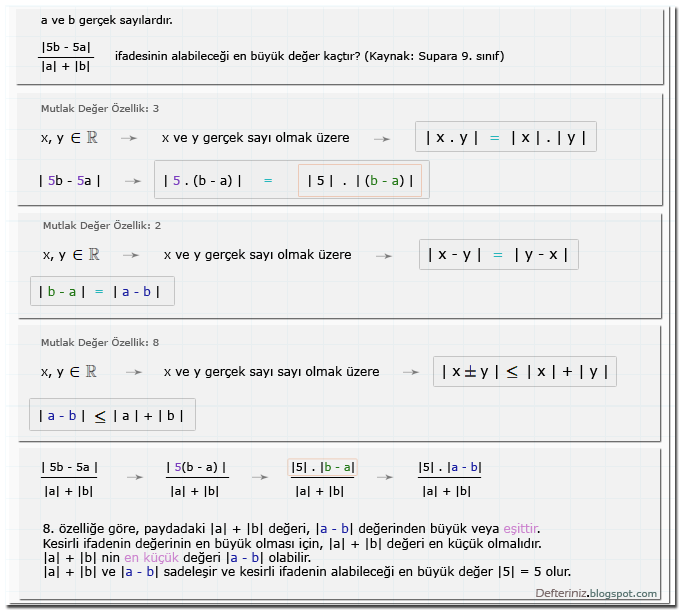
Örnek soru-3:
Mutlak değer özellik » Örnek soru-3 » İfadenin alabileceği en büyük değer (kaynak: Supara 9. sınıf):






Yorumlar
Yorum Gönder