Şu an 1. Bölüm görüntüleniyor...
Bir Sayının veya Bilinmeyenin Karesi
Pozitif Çift Tam Sayı Kuvvetleri (Üsleri)
Not:
Örnek-6 » Kesirli rasyonel sayıların kuvvetleri (üsleri):
Örnek Soru » Üslü sayılar ile toplama ve çıkarma işlemi (Kaynak: Supara 9. Sınıf):
Üslü Sayılar
Üslü Sayıların Tanımı
a Sayısının n. Kuvveti (Üssü)
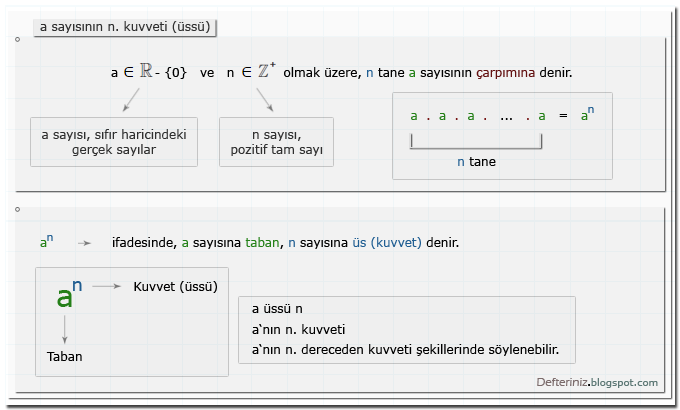
a ∈ R - {0} ve n ∈ Z⁺ olmak üzere, n tane, a sayısının çarpımına, a'nın n. kuvveti (üssü) denir.
a ∈ R - {0} → a sayısı, reel (gerçek) sayılar kümesinin sıfır kümesinden farkı kümesinin, elemanıdır. Başka bir ifadeyle, a sayısı, sıfır haricindeki gerçek sayılardır.
n ∈ Z⁺ → n sayısı, pozitif tam sayılar kümesinin elemanıdır.
a sayısının n. kuvveti (üssü):a ∈ R - {0} → a sayısı, reel (gerçek) sayılar kümesinin sıfır kümesinden farkı kümesinin, elemanıdır. Başka bir ifadeyle, a sayısı, sıfır haricindeki gerçek sayılardır.
n ∈ Z⁺ → n sayısı, pozitif tam sayılar kümesinin elemanıdır.
aⁿ ifadesinde, a sayısına taban, n sayısına kuvvet yada üs denir.
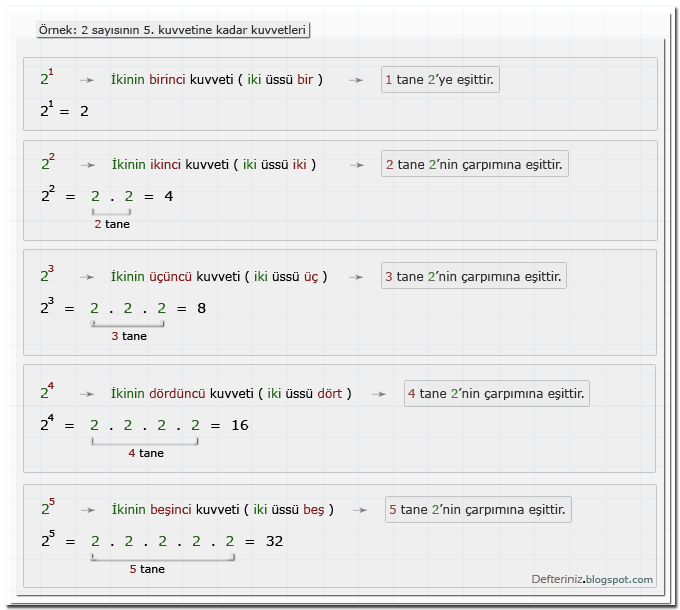
Örnek-1 » 2 sayısının 5. kuvvetine kadar kuvvetleri:- a üssü n
- a'nın n. kuvveti
- a'nın n. dereceden kuvveti
Bilinmeyen Kuvvetleri, Kare ve Küp Kavramları
Kuvvetleri alınan değerler, x, y ve z gibi bilinmeyen değerler de olabilir.
Örnek-2 » Bilinmeyen kuvvetleri, kare ve küp kavramları:-
xⁿ
x sayının n. kuvveti, n tane x sayısının çarpımına eşittir. -
yⁿ
y sayının n. kuvveti, n tane y sayısının çarpımına eşittir. -
zⁿ
z sayının n. kuvveti, n tane z sayısının çarpımına eşittir.
Bir Sayının veya Bilinmeyenin Karesi
Bir sayının veya bilinmeyenin ikinci kuvveti (üssü 2), karesi olarak da isimlendirilebilir. İkinci kuvveti alınan bilinmeyen ise, kare olarak da isimlendirilebilir.
Örneğin:
Bir Sayının veya Bilinmeyenin KüpüÖrneğin:
- 2² → 2'nin karesi
- 3² → 3'ün karesi
- 10² → 10'un karesi
- x² → x'in karesi veya x kare
- y² → y'nin karesi veya y kare
- z² → z'nin karesi veya z kare
- m² → m'nin karesi veya m kare
Bir sayının veya bilinmeyenin üçüncü kuvveti (üssü 3), küpü olarak da isimlendirilebilir. Üçüncü kuvveti alınan bilinmeyen ise, küp olarak da isimlendirilebilir.
Örneğin:
Not:Örneğin:
- 5³ → 5'in küpü
- 11³ → 11'in küpü
- 57³ → 57'nin küpü
- x³ → x'in küpü veya x küp
- y³ → y'nin küpü veya y küp
- z³ → z'nin küpü veya z küp
- m³ → m'nin küpü veya m küp
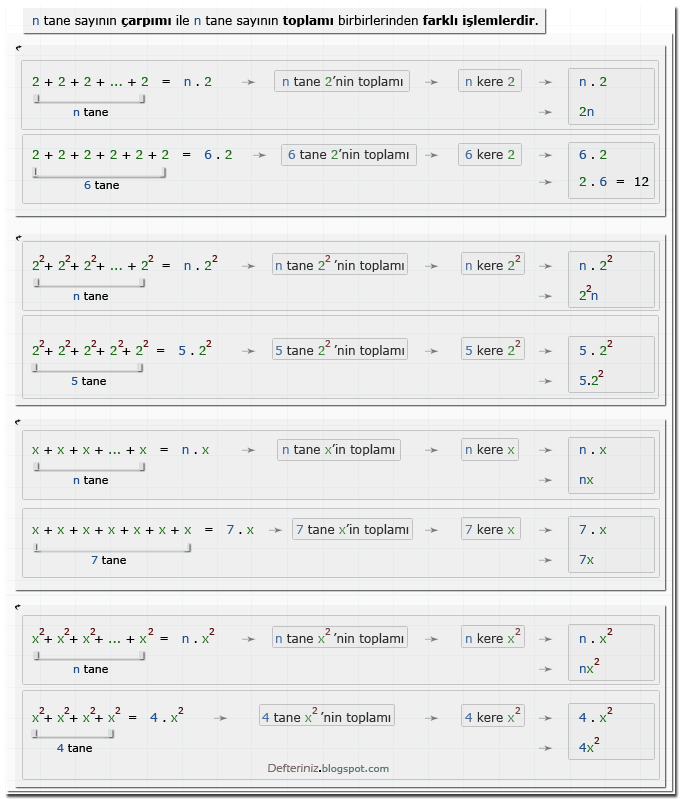
n tane sayının çarpımı ile n tane sayı toplamı birbirlerinden farklı işlemlerdir. Örneğin, 7 tane 2'nin toplamı işlemi, toplama ile yapılabileceği gibi, 7 . 2 = 14 işlemi ile de yapılabilir.
Farklı kat sayılara, aynı üsse sahip üslü sayılarda, toplama işlemine, özellikler bölümünde değinilecektir. Örnekte toplanan üslü sayıların kat sayıları 1'dir ve 1 kat sayısı, üslü sayıların önüne yazılmayabilir. Üslü örnekler için, yapılan toplama işleminin, yazılmayan 1 kat sayılarının toplanması olduğu söylenilebilir.
Örnek-3 » n tane sayının toplamı işlemi:Farklı kat sayılara, aynı üsse sahip üslü sayılarda, toplama işlemine, özellikler bölümünde değinilecektir. Örnekte toplanan üslü sayıların kat sayıları 1'dir ve 1 kat sayısı, üslü sayıların önüne yazılmayabilir. Üslü örnekler için, yapılan toplama işleminin, yazılmayan 1 kat sayılarının toplanması olduğu söylenilebilir.
Negatif a Gerçek Sayısının Pozitif Tek Tam Sayı ve Çift Tam Sayı Kuvvetleri (Üsleri)
Pozitif Tek Tam Sayı Kuvvetleri (Üsleri)
a ∈ R⁻ ve n ∈ pozitif tek tam sayı olmak üzere, aⁿ değeri negatiftir.
a ∈ R⁻ → a sayısı, negatif reel (gerçek) sayılar kümesinin elemanıdır.
n ∈ pozitif tek tam sayı → n sayısı, pozitif tek tam sayılar kümesinin elemanıdır.
Örnek-4 » Negatif a gerçek sayısının pozitif tek tam sayı sayı kuvvetleri (üsleri):a ∈ R⁻ → a sayısı, negatif reel (gerçek) sayılar kümesinin elemanıdır.
n ∈ pozitif tek tam sayı → n sayısı, pozitif tek tam sayılar kümesinin elemanıdır.
Pozitif Çift Tam Sayı Kuvvetleri (Üsleri)
a ∈ R⁻ ve n ∈ pozitif çift tam sayı olmak üzere, aⁿ değeri pozitiftir.
Örnek-5 » Negatif a gerçek sayısının pozitif çift tam sayı sayı kuvvetleri (üsleri):Not:
Negatif veya pozitif tüm reel sayıların çift kuvvetleri, pozitif ise, tüm sayıların kareleri (2. kuvvetleri) pozitiftir.
- 1² → 1 . 1 = 1
- (-1)² → (-1) . (-1) = 1
- 2² → 2 . 2 = 4
- (-2)² → (-2) . (-2) = 4
- (-1)³ → (-1) . (-1) . (-1) = -1
- (-2)³ → (-2) . (-2) . (-2) = -8
- 1³ → 1 . 1 . 1 = 1
- 2³ → 2 . 2 . 2 = 8
Kesirli Rasyonel Sayıların Kuvvetleri (Üsleri)
- n tane aynı kesirli sayının çarpımında, paylar çarpılıp paya, payda'lar çarpılıp payda'ya yazılabilir.
- Kesirli sayının kuvveti, hem payın hem de payda'nın kuvvetidir. Pay'ın kuvveti alınıp paya, payda'nın kuvveti alınıp payda'ya şeklinde de kesirli sayının kuvveti alınabilir.
- 1'e bölünen üslü sayılar, kesirli rasyonel sayı olarak adlandırılabilir. 1'e bölünen, üslü sayıların, üslerinin (-) işareti, 1'e bölünmesinden dolayıdır. Üsleri, (-) işaretli olan üslü sayılara, ayrıca değinilecektir.
Gerçek Sayıların 1. Kuvvetleri (Üsleri)
∀ a ∈ R olmak üzere, a¹ = a 'dır.
∀ → Sembolü, her (bütün) anlamındadır.
∀ a ∈ R → Reel sayılar kümesinin elemanı olan her (bütün) a sayıları
Her gerçek sayının 1. kuvveti kendisine eşittir. Başka bir ifade ile, her gerçek sayının üssü 1'dir ve 1 üssü yazılmayabilir.
Aynı tabana ait iki üslü sayının çarpma işleminde,
Örneğin:
2² . 2
şeklinde bir işlemde, 2 sayısının yazılmayan üssünün, 1 olduğunun bilinmesi açısından önemlidir.
2² . 2¹
Örnek-7 » Gerçek sayıların 1. kuvvetleri (üsleri):∀ → Sembolü, her (bütün) anlamındadır.
∀ a ∈ R → Reel sayılar kümesinin elemanı olan her (bütün) a sayıları
Her gerçek sayının 1. kuvveti kendisine eşittir. Başka bir ifade ile, her gerçek sayının üssü 1'dir ve 1 üssü yazılmayabilir.
Aynı tabana ait iki üslü sayının çarpma işleminde,
Örneğin:
2² . 2
şeklinde bir işlemde, 2 sayısının yazılmayan üssünün, 1 olduğunun bilinmesi açısından önemlidir.
2² . 2¹
Gerçek Sayıların 0. Kuvvetleri (Üsleri)
Sıfır haricindeki tüm gerçek sayıların, sıfırıncı kuvvetleri 1'eşittir. (-) işaretli üslü sayılar bölümünde konuya tekrar değinilecektir.
Örnek-8 » Gerçek sayıların 0. kuvvetleri (üsleri):Sıfır Sayısının 0. Kuvveti (Üssü)
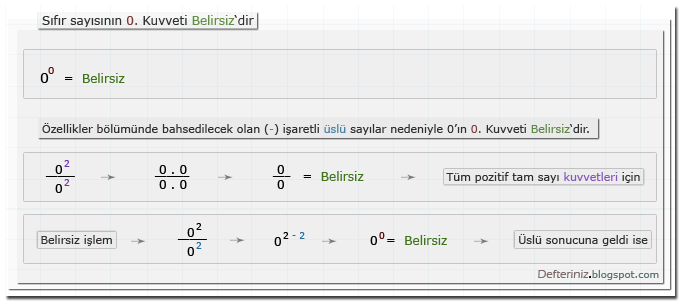
Sıfır sayısının, sıfırıncı kuvveti belirsizdir.
0⁰ → Belirsiz
Örnek-9 » Sıfır sayısının 0. kuvveti (üssü):0⁰ → Belirsiz
Örnek Soru » Üslü sayılar ile toplama ve çıkarma işlemi (Kaynak: Supara 9. Sınıf):







Yorumlar
Yorum Gönder