Şu an 1. Bölüm görüntüleniyor...
Bölüm Konuları:
Bölme İşlemi, Bölme İşlemi Örnekleri , Ondalık Sonuçlu Bölme İşlemi Örnekleri
Bölme İşleminin Özellikleri, Aynı Sayıya Bölünen Farklı İki Sayının Kalan İlişkileri
A , B , C , K doğal sayılar A ≥ B ≥ 1 olsun.
Yukarıdaki ifade;
A, B, C ve K sayılarının, doğal sayılar kümesinin elemanı olduğunu
B sayısının, 1 sayısına eşit veya 1 sayısından büyük olduğunu
A sayısının, B sayısına eşit veya B sayısından büyük olduğunu ifade eder.
A sayısının içinde, kaç tane B sayısı olduğu, bölme işlemi ile bulunur. Bulunan sonuç C harfi ile gösterilir. C kadar B sayısı, A sayısından çıktıktan sonra arta kalan sayı, K harfi ile gösterilir.
Yukarıdaki resimde:
A → Bölme işleminde, A harfinin bulunduğu yerdeki sayıya, bölünen sayı denir.
B → Bölme işleminde, B harfinin bulunduğu yerdeki sayıya, bölen sayı denir.
C → Bölme işleminde, C harfinin bulunduğu yerdeki sayı, bölüm (sonuç) olarak isimlendirilir.
K → Bölme işleminde, K harfinin bulunduğu yerdeki sayıya, kalan sayı denir. A sayısı, B sayısına tam bölünüyorsa, kalan sayı sıfır (0) olur.
Aynı resimde verilen örnekte:
10 → Bölünen sayı
2 → Bölen sayı
5 → Bölüm (sonuç)
0 → Kalan sayıdır.
Not:
> büyüktür sembolüdür. → (a > 5) ifadesi, a sayısı, 5 sayısından büyüktür anlamındadır.
< küçüktür sembolüdür. → (a < 5) ifadesi, a sayısı, 5 sayısından küçüktür anlamındadır.
≥ büyük eşit sembolüdür. → (a ≥ 5) ifadesi, a sayısı, 5 sayına eşit veya büyüktür anlamındadır.
≤ küçük eşit sembolüdür. → (a ≤ 5) ifadesi, a sayısı, 5 sayına eşit veya küçüktür anlamındadır.
100 sayısının, 8 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 100'dür. 100 sayısının en solunda bulunan rakam 1'dir. 1 sayısının içinde, bölen sayı olan 8 olmadığı için, bölme işlemine 100 sayısının, sol tarafında olan 10 sayısından başlanır.
Kalan : 4
Örnek 2:
489 sayısının, 23 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 489'dur. 489 sayısının en solunda bulunan rakam 4'dür. 4 sayısının içinde, bölen sayı olan 23 olmadığı için, bölme işlemine 489 sayısının, sol tarafında olan 48 sayısından başlanır.
Kalan : 6
Örnek 3:
791 sayısının, 19 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 791'dir. 791 sayısının en solunda bulunan rakam 7'dir. 7 sayısının içinde, bölen sayı olan 19 olmadığı için, bölme işlemine 791 sayısının, sol tarafında olan 79 sayısından başlanır.
Kalan : 12
Örnek 4:
407 sayısının, 17 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 407'dir. 407 sayısının en solunda bulunan rakam 4'dür. 4 sayısının içinde, bölen sayı olan 17 olmadığı için, bölme işlemine 407 sayısının, sol tarafında olan 40 sayısından başlanır.
Kalan : 16
Örnek 1:
96 sayısının, 80 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 96'dır. 96 sayısının en solunda bulunan rakam 9'dur. 9 sayısının içinde, bölen sayı olan 80 olmadığı için, bölme işlemine 96 sayısından başlanır.
Kalan : 0
Örnek 2:
75 sayısının, 60 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 75'dir. 75 sayısının en solunda bulunan rakam 7'dir. 7 sayısının içinde, bölen sayı olan 60 olmadığı için, bölme işlemine 75 sayısından başlanır.
Kalan : 0
Örnek 3:
21 sayısının, 20 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 21'dir. 21 sayısının en solunda bulunan rakam 2'dir. 2 sayısının içinde, bölen sayı olan 20 olmadığı için, bölme işlemine 21 sayısından başlanır.
Kalan : 0
Bazı bölme işlemlerinde virgülden sonraki sonuç, aynı rakamların tekrarı (devri) şeklinde sonsuz rakamdan oluşur. Örneğin ( 20 / 6 ) işleminde sonuç 6,666.... şeklinde sonsuza uzanır. 6,666... sonucu, virgülden sonra devreden 6 rakamlarından ilkinin üst tarafına, çizgi konularak, 6,6 şeklinde yazılır. Devirli ondalık sonuçlu bölme işlemine, Sayılar 4. Bölüm » başlıklı yazıda değinilmiştir.
Yukarıdaki resimde belirtilen A, B, C ve K sayıları için:
A = B . C + K → Bölünen sayı, bölen sayı ile bölüm'ün çarpımının, kalan sayı ile toplanmasına eşittir.
Bölme işleminin özellikleri (A = B . C + K):
(23 / 5) işleminde:
Bölünen sayı (A) = 23
Bölen sayı (B) = 5
Bölüm (C) = 4
Kalan sayı (K) = 3'tür.
A = B . C + K
23 = 5 . 4 + 3 = 20 + 3 = 23
Bu örnekte, bölen sayı verilmemiş olsun. Verilmeyen bölen sayıya x diyelim.
23 = x . 4 + 3 → denklemi kurulur.
23 - 3 = 4x → (+3) sayısı, eşitliğin diğer tarafına geçtiğinde (-3) olur. (x . 4) ifadesi, 4x şeklinde yazılabilir.
20 = 4x → Eşitliğinde, eşitliğin her iki tarafı, 4 sayısına bölünür.
5 = x → 20 sayısı, 4'e bölündüğünde 5 olur. 4x ifadesi, 4'e bölündüğünde, 4 sayıları sadeleşir ve x yalnız kalır.
Bölen sayı verilmemiş olsa bile, verilen sayı değerleri, formülde yerine konularak, bölen sayı bulunabilir. Bölünen sayı, bölüm ve kalan sayı değerleri de formül aracılığı ile bulunabilir.
C < B → Bölme işleminde, bölen sayı, kalan sayıdan büyüktür. Bölme işlemi sonuçlandıysa, bölen sayı, kalan sayıdan büyük olmalıdır. Kalan bölümünde olan sayı, bölen sayıdan büyükse, bölme işlemi devam ediyor demektir.
K < C ise, B ile C yer değiştirebilir. Kalan sayı yine K olur → Bölme işleminde; bölüm (sonuç), kalan sayıdan büyük ise, bölüm ve bölen sayı yer değiştirebilir.
Bölme işleminin özellikleri (K < C ise, B ile C yer değiştirebilir. Kalan sayı yine K olur):
(23 / 5) işleminde:
Bölüm (C) = 4
Kalan sayı (K) = 3'tür ve bölüm, kalan sayıdan büyüktür. ( 3 < 4 )
Bu koşula göre, bölen sayı ve bölüm yer değiştirebilir. (23 / 5) işlemi için, bölen sayı ve bölüm yer değiştirirse, yapılan yeni işlem (23 / 4) işlemi olur.
(23 / 4) işleminde:
Bölüm (C) = 5
Kalan sayı (K) = yine 3'tür ve yine bölüm, kalan sayıdan büyüktür. (3 < 5)
5 . 4 + 3 = 4 . 5 + 3
Bölme işleminin özellikleri, (23 / 10) işlemi için:
(23 / 10) işleminde:
Bölüm (C) = 2
Kalan sayı (K) = 3'tür ve bu işlemde bölüm, kalan sayıdan küçüktür. ( 2 < 3 )
Bu koşula göre, bölen sayı ve bölüm yer değiştirse, kalan sayı, yapılan iki işlem için, birbirinden farklı olur.
(23 / 10) işlemi için, bölen sayı ve bölüm yer değiştirirse, yapılan yeni işlem (23 / 2) işlemi olur.
(23 / 2) işleminde:
Bölüm (C) = 11
Kalan sayı (K) = 1 olur.
10 . 2 + 3 = 2 . 11 + 1
K = 0 ise, A sayısı, B sayısına tam bölünür → Bölme işleminde, kalan sayı sıfır ise, bölünen sayı, bölen sayıya tam bölünür.
Not:
Bölme işleminde kalan sayı, bölen sayıdan küçüktür. ( K < B )
Kalan sayı sıfıra eşit veya sıfırdan büyük, bölen sayıdan küçüktür. ( 0 ≤ K < B )
Bölme işleminin özellikleri (K = 0 ise, A sayısı, B sayısına tam bölünür):
(30 / 6) işleminde:
Bölünen sayı (A) = 30
Bölen sayı (B) = 6
Bölüm (C) = 5
Kalan sayı (K) = 0 (Sıfırdır)
30 = 6 . 5 + 0 = 30 + 0 = 30
K = 0 ise
B sayısı, A sayısının tam bölenidir.
K = 0 ise, K < C 'dir ve bölüm ile bölünen sayı yer değiştirebilir.
B sayısı, A sayısının tam böleni ise, C sayısı da A sayısının tam bölenidir.
Örnek:
Bölme işlemi formül örnek soru (Kaynak: Supara):
Çözüm:
A = B . C + K formülünün açılımı:
Bölünen sayı = (Bölen sayı) . (Bölüm) + Kalan sayı
Bölme işlemi formül örnek soru çözümü:
Birinci bölme işlemi için:
a → Bölünen
b → bölen
2 → bölüm
3 → kalan ise,
a = b . 2 + 3 → (b . 2) ifadesi 2b şeklinde yazılırsa → a = 2b + 3
İkinci bölme işlemi için:
b → Bölünen
c → bölen
3 → bölüm
2 → kalan ise,
b = c . 3 + 2 → (c . 3) ifadesi 3c şeklinde yazılırsa → b = 3c + 2
a = 2b + 3 → ifadesinde b yerine, ikinci bölme işleminde bulunan b değeri olan (3c + 2) yazılır.
a = 2(3c + 2) + 3 → b yerine, ikinci bölme işleminde bulunan b değeri olan (3c + 2) yazıldığında oluşan yeni eşitlik
a = 2(3c + 2) + 3 işlemi için önce parantez açma işlemi yapılır.
2(3c + 2) parantezi, parantez dışında bulunan 2 sayısı ile açılır.
2 ile 3c çarpılır → 2 . 3c = 6c
2 ile 2 çarpılır → 2 . 2 = 4
Parentez içindeki (+) işareti, 6c ve 4 değerleri arasında bırakılır. → 6c + 4
Parantez işleminden sonra, 3 ile toplama işlemi yapılır. → 6c + 4 + 3 → 6c + 7
a = 6c + 7 olur.
Cevap: 6c + 7
Örnek:
Bölme işlemi örnek soru (kaynak: Supara)
Çözüm:
Bir bölme işleminde; kalan sayı (K), bölen sayıdan (B) küçük olmalıdır.
K < B
Bölünen sayı (A) tam bölünüyorsa; kalan sayı (K) sıfır olmalıdır.
Soruda verilen bölme işlemi için:
Bölen sayı (B) = 25
Bölüm (C) (Sonuç) = x + 4
Kalan sayı (K) = x²
Soruda, x sayısı tam sayı olarak tanımlanmıştır. Tam sayılar kümesi (-) negatif sayıları da içerir.
x² < 25 → K < B
x = (-4) için
x² = (-4) . (-4) = 16
Bölüm (C) = (x + 4) = (-4) + 4 = 0
x = (-3) için
x² = (-3) . (-3) = 9
Bölüm (C) = (x + 4) = (-3) + 4 = 1
x = (-2) için
x² = (-2) . (-2) = 4
Bölüm (C) = (x + 4) = (-2) + 4 = 2
x = (-1) için
x² = (-1) . (-1) = 1
Bölüm (C) = (x + 4) = (-1) + 4 = 3
x = 0 için
x² = 0 . 0 = 0
Bölüm (C) = (x + 4) = 0 + 4 = 4
x = 1 için
x² = 1 . 1 = 1
Bölüm (C) = (x + 4) = 1 + 4 = 5
x = 2 için
x² = 2 . 2 = 4
Bölüm (C) = (x + 4) = 2 + 4 = 6
x = 3 için
x² = 3 . 3 = 9
Bölüm (C) = (x + 4) = 3 + 4 = 7
x = 4 için
x² = 4 . 4 = 16
Bölüm (C) = (x + 4) = 4 + 4 = 8
x sayısının, (-4, -3, -2, -1, 0 , 1 , 2 , 3 ve 4) değerleri için x² < 25 koşulu sağlanır.
x = (-4) değeri için, bölüm (C) = 0 olur. (x + 4 = (-4) + 4 = 0)
Bir bölme işleminin sonucu sıfır (0) ise, bölünen sayı sıfır (0) olmalıdır. Sonuç sıfır (0) ise, kalan sayı da sıfır (0) olmalıdır.
x² = (-4) . (-4) = 16 kalan sayı değeri, sıfır (0) sonucu için mümkün olamaz.
Not:
Sıfır (0) sayısı, sıfır haricinde hangi sayıya bölünürse bölünsün, sonuç ve kalan sıfır (0) olur.
0 / 1 işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / (-5) işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / ∛5 işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / (-√3) işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / 0 işlemi belirsiz bir işlemdir.
1 / 0 işlemi tanımsız bir işlemdir. (Sıfır hariç, tüm sayıların sıfıra (0) bölümü tanımsızdır.)
x = (-4) olamayacağı için, x sayısı 8 farklı değer alabilir. x sayısının 8 farklı değeri için, A sayısı da 8 farklı değer alır.
Cevap : 8
y sayısının a ile bölümünden kalan n
olmak üzere:
(x ± y)'nin a ile bölümünden kalan (m ± n)'dir
Yukarıdaki ifade;
Birinci sayı olan x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
İkinci sayı olan y sayısının, yine a sayısına bölünmesi ile kalan sayının n olduğunu
Birinci sayı olan x ile ikinci sayı olan y'nin toplamının veya farkının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile y işleminin kalanı olan n'nin toplamı veya farkı olacağını ifade eder.
± → Sembolü ile verilen önermenin, hem toplama işlemi için hem çıkarma işlemi için geçerli olduğunu ifade edilir.
(x ± y)'nin a ile bölümünden kalan (m ± n)'dir:
Kalanların toplamı, bölen sayıdan küçükse:
Birinci sayı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İkinci sayı 34 olur ise, 34 sayısının, 8 sayısına bölümünden kalan, 2 olur.
Kurala göre, 41 ile 34'ün toplamının, 8 sayısına bölümünden kalan ( 2 + 1 = 3) olmalıdır.
Kalan sayıların toplamı olan 3, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 + 34 = 75
75 sayısının 8 ile bölümünden kalan 3 olur.
Kalanların toplamı, bölen sayıdan büyükse:
Birinci sayı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
İkinci sayı 52 olur ise, 52 sayısının, 8 sayısına bölümünden kalan, 4 olur.
Kurala göre, 47 ile 52'in toplamının, 8 sayısına bölümünden kalan ( 7 + 4 = 11) olmalıdır.
Kalan sayıların toplamı olan 11, bölen sayı olan 8'den büyük olduğu için 11 sayısı, tekrar 8 sayısına bölünür.
11 sayısının, 8 sayısına bölümünden kalan, 3 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 + 52 = 99
99 sayısının 8 ile bölümünden kalan 3 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 2 ise
(a - b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4'ten, b sayısının 5 ile bölümünden kalan sayı olan 2 çıkarılırsa, (a - b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 - 2 = 2
Bulunan 2 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 3 ise
(a + b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4 ile b sayısının 5 ile bölümünden kalan sayı olan 3 toplanırsa, (a + b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 + 3 = 7
Kalan sayıların toplamı olan 7, bölen sayı olan 5 sayısından büyük olduğundan; 7 sayısı, 5 sayısına bölünür.
7 sayısının, 5 sayısına bölümünden kalan, 2 olur.
Cevap : 2
(x . y)'nin a ile bölümünden kalan (m . n)'dir
Yukarıdaki ifade;
Birinci sayı olan x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
İkinci sayı olan y sayısının, yine a sayısına bölünmesi ile kalan sayının n olduğunu
Birinci sayı olan x ile ikinci sayı olan y'nin çarpımının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile y işleminin kalanı olan n'nin çarpımı olacağını ifade eder.
(x . y)'nin a ile bölümünden kalan (m . n)'dir:
Kalanların çarpımı, bölen sayıdan küçükse:
Birinci sayı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İkinci sayı 34 olur ise, 34 sayısının, 8 sayısına bölümünden kalan, 2 olur.
Kurala göre, 41 ile 34'ün çarpımının, 8 sayısına bölümünden kalan ( 2 . 1 = 2) olmalıdır.
Kalan sayıların çarpımı olan 2, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 . 34 = 1394
1394 sayısının 8 ile bölümünden kalan 2 olur.
Kalanların çarpımı, bölen sayıdan büyükse:
Birinci sayı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
İkinci sayı 52 olur ise, 52 sayısının, 8 sayısına bölümünden kalan, 4 olur.
Kurala göre, 47 ile 52'in çarpımının, 8 sayısına bölümünden kalan ( 7 . 4 = 28) olmalıdır.
Kalan sayıların çarpımı olan 28, bölen sayı olan 8'den büyük olduğu için 28 sayısı, tekrar 8 sayısına bölünür.
28 sayısının, 8 sayısına bölümünden kalan, 4 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 . 52 = 2444
2444 sayısının 8 ile bölümünden kalan 4 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 1
b sayısının 5 ile bölümünden kalan 2 ise
(a . b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 1 ile, b sayısının 5 ile bölümünden kalan sayı olan 2 çarpılırsa, (a . b) sayısının 5 ile bölümünden kalan sayı bulunur.
1 . 2 = 2
Bulunan 2 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 3 ise
(a . b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4 ile, b sayısının 5 ile bölümünden kalan sayı olan 3 çarpılırsa, (a . b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 . 3 = 12
Kalan sayıların çarpımı olan 12, bölen sayı olan 5 sayısından büyük olduğundan; 12 sayısı, 5 sayısına bölünür.
12 sayısının, 5 sayısına bölümünden kalan, 2 olur.
Cevap : 2
(t . x)'nin a ile bölümünden kalan (t . m)'dir
Yukarıdaki ifade;
x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
x sayısı ile t sayının çarpımının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile t sayısının çarpımı olacağını ifade eder.
(t . x)'nin a ile bölümünden kalan (t . m)'dir:
t sayısı ile kalan sayının çarpımı, bölen sayıdan küçükse:
x sayısı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
t sayısı 3 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre, 41 ile t sayısı olan 3'ün çarpımının, 8 sayısına bölümünden kalan ( 1 . 3 = 3) olmalıdır.
Kalan sayı ile t sayısının çarpımı olan 3, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 . 3 = 123
123 sayısının 8 ile bölümünden kalan 3 olur.
t sayısı ile kalan sayının çarpımı, bölen sayıdan büyükse:
x sayısı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre, 47 ile t sayısı olan 2'nin çarpımının, 8 sayısına bölümünden kalan ( 7 . 2 = 14) olmalıdır.
Kalan sayı ile t sayısının çarpımı olan 14, bölen sayı olan 8'den büyük olduğu için 14 sayısı, tekrar 8 sayısına bölünür.
14 sayısının, 8 sayısına bölümünden kalan, 6 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 . 2 = 94
94 sayısının 8 ile bölümünden kalan 6 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 1'dir.
a sayısının 4 katının, 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı 1 ise,
a sayısının dört katının 5 ile bölümünden kalan sayı,
a sayısının 5 ile bölümünden kalan sayı olan 1'in dört katıdır.
1 . 4 = 4
Bulunan 4 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4'dür.
a sayısının 102 katının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı 4 ise,
a sayısının 102 katının 5 ile bölümünden kalan sayı,
a sayısının 5 ile bölümünden kalan sayı olan 4'ün 102 katıdır.
4 . 102 = 408
Kalan sayı ile t sayısının çarpımı olan 408, bölen sayı olan 5 sayısından büyük olduğundan; 408 sayısı, 5 sayısına bölünür.
408 sayısının, 5 sayısına bölümünden kalan, 3 olur.
Cevap : 3
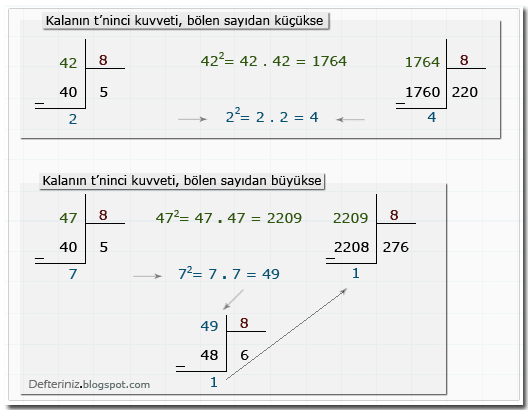
x'in t'ninci kuvvetinin a ile bölümünden kalan, m'nin t'ninci kuvvetidir
Yukarıdaki ifade;
x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
x sayısının t'ninci kuvvetinin, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m sayısının, t'ninci kuvveti olduğunu ifade eder.
x'in t'ninci kuvvetinin a ile bölümünden kalan, m'nin t'ninci kuvvetidir:
Kalan sayının t'ninci kuvveti, bölen sayıdan küçükse:
x sayısı 42 olur ise, 42 sayısının, 8 sayısına bölümünden kalan, 2 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre:
42 sayısının, 8 sayısına bölümünden kalan sayı olan 2'nin 2. kuvveti (2²),
42 sayısının 2. kuvvetinin (42²), 8 sayısına bölümünden kalan sayıdır. (2² = 2 . 2 = 4 )
Kalan sayının 2. kuvveti olan 4, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
42² = 42 . 42 = 1764
1764 sayısının 8 ile bölümünden kalan 4 olur.
Kalan sayının t'ninci kuvveti, bölen sayıdan büyükse:
x sayısı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre:
47 sayısının, 8 sayısına bölümünden kalan sayı olan 7'nin 2. kuvveti (7²),
47 sayısının 2. kuvvetinin (47²), 8 sayısına bölümünden kalan sayıdır. (7² = 7 . 7 = 49 )
Kalan sayının 2. kuvveti olan 49, bölen sayı olan 8'den büyük olduğu için 49 sayısı, tekrar 8 sayısına bölünür.
49 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47² = 47 . 47 = 2209
2209 sayısının 8 ile bölümünden kalan 1 olur.
Örnek:
a sayısının, 9 ile bölümünden kalan 2 ise
a³ sayısının, 9 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 9 ile bölümünden kalan sayı 2 ise,
a sayısının 3.kuvvetinin 9 ile bölümünden kalan sayı,
a sayısının 9 ile bölümünden kalan sayı olan 2'nin 3.kuvvetidir.
2³ = 2 . 2 . 2 = 8
Bulunan 8 sayısı, bölen sayı olan 9'dan küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 9 ile bölümünden kalan 2 ise
a⁵ sayısının, 9 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 9 ile bölümünden kalan sayı 2 ise,
a sayısının 5.kuvvetinin 9 ile bölümünden kalan sayı,
a sayısının 9 ile bölümünden kalan sayı olan 2'nin 5.kuvvetidir.
2⁵ = 2 . 2 . 2 . 2 . 2 = 32
Kalan sayının 5. kuvveti olan 32, bölen sayı olan 9 sayısından büyük olduğundan; 32 sayısı, 9 sayısına bölünür.
32 sayısının, 9 sayısına bölümünden kalan, 5 olur.
Cevap : 5
Örnek:
x ve y pozitif tam sayılardır.
x in 6 ile bölümünden kalan 2,
y nin 6 ile bölümünden kalan 5 olduğuna göre
x.y + y² nin 6 ile bölümünden kalan kaçtır? (Kaynak: Supara)
Çözüm:
Aynı sayıya bölünen sayıların kalan ilişkilerinde, toplama ve çarpma işlemi (veya diğer işlemler) birlikte kullanılıyorsa, işlemler kalan sayılar ile yapılır.
x in 6 ile bölümünden kalan 2 ise (x.y + y²) işleminde, x yerine 2 yazılır. (x = 2)
y nin 6 ile bölümünden kalan 5 ise (x.y + y²) işleminde, y yerine 5 yazılır. (y = 5)
x = 2
y = 5 için
x.y + y² = 2 . 5 + 5² = 10 + 25 = 35
Çıkan sonuç 6 sayısından küçük olsaydı, bulunan sonuç, (x.y + y²) işleminin, 6 ile bölümünden kalan olacaktı.
Çıkan sonuç olan 35 sayısı, 6 sayısından büyük olduğundan, (x.y + y²) işleminin, 6 ile bölümünden kalan:
35 sayısının 6 ile bölümünden kalandır. 35 sayısı, 6 ile bölündüğünde kalan sayı 5 olur.
Cevap: 5
Bölüm Konuları:
Bölme İşlemi, Bölme İşlemi Örnekleri , Ondalık Sonuçlu Bölme İşlemi Örnekleri
Bölme İşleminin Özellikleri, Aynı Sayıya Bölünen Farklı İki Sayının Kalan İlişkileri
Bölme İşlemi
Bölme işlemi:A , B , C , K doğal sayılar A ≥ B ≥ 1 olsun.
Yukarıdaki ifade;
A, B, C ve K sayılarının, doğal sayılar kümesinin elemanı olduğunu
B sayısının, 1 sayısına eşit veya 1 sayısından büyük olduğunu
A sayısının, B sayısına eşit veya B sayısından büyük olduğunu ifade eder.
A sayısının içinde, kaç tane B sayısı olduğu, bölme işlemi ile bulunur. Bulunan sonuç C harfi ile gösterilir. C kadar B sayısı, A sayısından çıktıktan sonra arta kalan sayı, K harfi ile gösterilir.
Yukarıdaki resimde:
A → Bölme işleminde, A harfinin bulunduğu yerdeki sayıya, bölünen sayı denir.
B → Bölme işleminde, B harfinin bulunduğu yerdeki sayıya, bölen sayı denir.
C → Bölme işleminde, C harfinin bulunduğu yerdeki sayı, bölüm (sonuç) olarak isimlendirilir.
K → Bölme işleminde, K harfinin bulunduğu yerdeki sayıya, kalan sayı denir. A sayısı, B sayısına tam bölünüyorsa, kalan sayı sıfır (0) olur.
Aynı resimde verilen örnekte:
10 → Bölünen sayı
2 → Bölen sayı
5 → Bölüm (sonuç)
0 → Kalan sayıdır.
Not:
> büyüktür sembolüdür. → (a > 5) ifadesi, a sayısı, 5 sayısından büyüktür anlamındadır.
< küçüktür sembolüdür. → (a < 5) ifadesi, a sayısı, 5 sayısından küçüktür anlamındadır.
≥ büyük eşit sembolüdür. → (a ≥ 5) ifadesi, a sayısı, 5 sayına eşit veya büyüktür anlamındadır.
≤ küçük eşit sembolüdür. → (a ≤ 5) ifadesi, a sayısı, 5 sayına eşit veya küçüktür anlamındadır.
Bölme İşlemi Örnekleri
Örnek 1:100 sayısının, 8 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 100'dür. 100 sayısının en solunda bulunan rakam 1'dir. 1 sayısının içinde, bölen sayı olan 8 olmadığı için, bölme işlemine 100 sayısının, sol tarafında olan 10 sayısından başlanır.
- 10 sayısının içinde, 1 tane 8 vardır.
- 1 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 1 ile bölen sayı çarpılır. ( 1 . 8 = 8 )
- Bulunan sonuç 10 sayısından çıkarılır. ( 10 - 8 = 2 )
- 2 sayısı kalan kısmına yazılır.
- 100 sayısında kullanılmayan rakam olduğu için işlem devam eder.
- 2 sayısının içinde 8 yok.
- 100 sayısının en sağında bulunan sıfır rakamı, 2 sayısının sağına iner.
- Kalan kısmında 20 sayısı olur.
- 20 sayısının içinde 2 tane 8 vardır.
- 2 sayısı, bölüm kısmında olan 1 sayısının sağına yazılır.
- Bölüm kısmında 12 sayısı olur.
- Bölüm kısmına eklenen 2 sayısı ile bölen sayı çarpılır ( 2 . 8 = 16 )
- Bulunan sonuç 20 sayısından çıkarılır. ( 20 - 16 = 4 )
- 4 sayısının içinde, 8 yok.
- 100 sayısının tüm rakamları kullanıldığı için işlem biter.
Kalan : 4
Örnek 2:
489 sayısının, 23 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 489'dur. 489 sayısının en solunda bulunan rakam 4'dür. 4 sayısının içinde, bölen sayı olan 23 olmadığı için, bölme işlemine 489 sayısının, sol tarafında olan 48 sayısından başlanır.
- 48 sayısının içinde, 2 tane 23 vardır.
- 2 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 2 ile bölen sayı çarpılır. ( 2 . 23 = 46 )
- Bulunan sonuç 48 sayısından çıkarılır. ( 48 - 46 = 2 )
- 2 sayısı kalan kısmına yazılır.
- 489 sayısında kullanılmayan rakam olduğu için işlem devam eder.
- 2 sayısının içinde 23 yok.
- 489 sayısının en sağında bulunan 9 rakamı, 2 sayısının sağına iner.
- Kalan kısmında 29 sayısı olur.
- 29 sayısının içinde 1 tane 23 vardır.
- 1 sayısı, bölüm kısmında olan 2 sayısının sağına yazılır.
- Bölüm kısmında 21 sayısı olur.
- Bölüm kısmına eklenen 1 sayısı ile bölen sayı çarpılır ( 1 . 23 = 23 )
- Bulunan sonuç 29 sayısından çıkarılır. ( 29 - 23 = 6 )
- 6 sayısının içinde, 23 yok.
- 489 sayısının tüm rakamları kullanıldığı için işlem biter.
Kalan : 6
Örnek 3:
791 sayısının, 19 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 791'dir. 791 sayısının en solunda bulunan rakam 7'dir. 7 sayısının içinde, bölen sayı olan 19 olmadığı için, bölme işlemine 791 sayısının, sol tarafında olan 79 sayısından başlanır.
- 79 sayısının içinde, 4 tane 19 vardır.
- 4 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 4 ile bölen sayı çarpılır. ( 4 . 19 = 76 )
- Bulunan sonuç 79 sayısından çıkarılır. ( 79 - 76 = 3 )
- 3 sayısı kalan kısmına yazılır.
- 791 sayısında kullanılmayan rakam olduğu için işlem devam eder.
- 3 sayısının içinde 19 yok.
- 791 sayısının en sağında bulunan 1 rakamı, 3 sayısının sağına iner.
- Kalan kısmında 31 sayısı olur.
- 31 sayısının içinde 1 tane 19 vardır.
- 1 sayısı, bölüm kısmında olan 4 sayısının sağına yazılır.
- Bölüm kısmında 41 sayısı olur.
- Bölüm kısmına eklenen 1 sayısı ile bölen sayı çarpılır ( 1 . 19 = 19 )
- Bulunan sonuç 31 sayısından çıkarılır. ( 31 - 19 = 12 )
- 12 sayısının içinde, 19 yok.
- 791 sayısının tüm rakamları kullanıldığı için işlem biter.
Kalan : 12
Örnek 4:
407 sayısının, 17 sayısına bölünmesi - bölme işlemi örneği:
Bölünen sayı 407'dir. 407 sayısının en solunda bulunan rakam 4'dür. 4 sayısının içinde, bölen sayı olan 17 olmadığı için, bölme işlemine 407 sayısının, sol tarafında olan 40 sayısından başlanır.
- 40 sayısının içinde, 2 tane 17 vardır.
- 2 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 2 ile bölen sayı çarpılır. ( 2 . 17 = 34 )
- Bulunan sonuç 40 sayısından çıkarılır. ( 40 - 34 = 6 )
- 6 sayısı kalan kısmına yazılır.
- 407 sayısında kullanılmayan rakam olduğu için işlem devam eder.
- 6 sayısının içinde 17 yok.
- 407 sayısının en sağında bulunan 7 rakamı, 6 sayısının sağına iner.
- Kalan kısmında 67 sayısı olur.
- 67 sayısının içinde 3 tane 17 vardır.
- 3 sayısı, bölüm kısmında olan 2 sayısının sağına yazılır.
- Bölüm kısmında 23 sayısı olur.
- Bölüm kısmına eklenen 3 sayısı ile bölen sayı çarpılır ( 3 . 17 = 51 )
- Bulunan sonuç 67 sayısından çıkarılır. ( 67 - 51 = 16 )
- 16 sayısının içinde, 17 yok.
- 407 sayısının tüm rakamları kullanıldığı için işlem biter.
Kalan : 16
Ondalık Sonuçlu Bölme İşlemi Örnekleri
Bölme işlemine, bölünen sayının tüm rakamları kullanıldıktan sonra, kalan sayının sağına sıfır (0) eklenerek devam edebilir. İşlemin devamı için bölüm (sonuç) kısmının sağına, virgül (,) eklenir. Kalan sayı sıfır (0) olana kadar işlem devam eder. Bulunan sonuç ondalık sayı şeklinde olur.Örnek 1:
96 sayısının, 80 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 96'dır. 96 sayısının en solunda bulunan rakam 9'dur. 9 sayısının içinde, bölen sayı olan 80 olmadığı için, bölme işlemine 96 sayısından başlanır.
- 96 sayısının içinde, 1 tane 80 vardır.
- 1 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 1 ile bölen sayı çarpılır. ( 1 . 80 = 80 )
- Bulunan sonuç 96 sayısından çıkarılır. ( 96 - 80 = 16 )
- 16 sayısı kalan kısmına yazılır.
- 16 sayısının içinde 80 olmadığı için, 16'nın sağına bir tane 0 eklenir.
- Kalan kısmında 160 sayısı olur.
- Bölüm kısmında bulunan 1 sayısının sağına virgül eklenir. ( 1, )
- 160 sayısının içinde, 2 tane 80 vardır.
- 2 sayısı, bölüm kısmında olan 1, sayısının sağına yazılır.
- Bölüm kısmında 1,2 sayısı olur.
- Bölüm kısmına eklenen 2 sayısı ile bölen sayı çarpılır ( 2 . 80 = 160 )
- Bulunan sonuç, bölünmeye devam eden 160 sayısından çıkarılır. ( 160 - 160 = 0 )
- Kalan sayı sıfır (0) olduğu için işlem biter.
Kalan : 0
Örnek 2:
75 sayısının, 60 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 75'dir. 75 sayısının en solunda bulunan rakam 7'dir. 7 sayısının içinde, bölen sayı olan 60 olmadığı için, bölme işlemine 75 sayısından başlanır.
- 75 sayısının içinde, 1 tane 60 vardır.
- 1 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 1 ile bölen sayı çarpılır. ( 1 . 60 = 60 )
- Bulunan sonuç 75 sayısından çıkarılır. ( 75 - 60 = 15 )
- 15 sayısı kalan kısmına yazılır.
- 15 sayısının içinde 60 olmadığı için, 15'in sağına bir tane 0 eklenir.
- Kalan kısmında 150 sayısı olur.
- Bölüm kısmında bulunan 1 sayısının sağına virgül eklenir. ( 1, )
- 150 sayısının içinde, 2 tane 60 vardır.
- 2 sayısı, bölüm kısmında olan 1, sayısının sağına yazılır.
- Bölüm kısmında 1,2 sayısı olur.
- Bölüm kısmına eklenen 2 sayısı ile bölen sayı çarpılır ( 2 . 60 = 120 )
- Bulunan sonuç, bölünmeye devam eden 150 sayısından çıkarılır. ( 150 - 120 = 30 )
- 30 sayısı kalan kısmına yazılır.
- 30 sayısının içinde 60 olmadığı için, 30'un sağına bir tane 0 eklenir.
- Kalan kısmında 300 sayısı olur.
- 300 sayısının içinde, 5 tane 60 vardır.
- 5 sayısı, bölüm kısmında olan 1,2 sayısının sağına yazılır.
- Bölüm kısmında 1,25 sayısı olur.
- Bölüm kısmına eklenen 5 sayısı ile bölen sayı çarpılır ( 5 . 60 = 300 )
- Bulunan sonuç 300 sayısından çıkarılır. ( 300 - 300 = 0 )
- Kalan sayı sıfır (0) olduğu için işlem biter.
Kalan : 0
Örnek 3:
21 sayısının, 20 sayısına bölünmesi - ondalık sonuçlu bölme işlemi örneği:
Bölünen sayı 21'dir. 21 sayısının en solunda bulunan rakam 2'dir. 2 sayısının içinde, bölen sayı olan 20 olmadığı için, bölme işlemine 21 sayısından başlanır.
- 21 sayısının içinde, 1 tane 20 vardır.
- 1 sayısı, bölüm kısmına yazılır.
- Bölüm kısmına yazılan 1 ile bölen sayı çarpılır. ( 1 . 20 = 20 )
- Bulunan sonuç 21 sayısından çıkarılır. ( 21 - 20 = 1 )
- 1 sayısı kalan kısmına yazılır.
- 1 sayısının içinde 20 olmadığı için, 1'in sağına bir tane 0 eklenir.
- Kalan kısmında 10 sayısı olur.
- Bölüm kısmında bulunan 1 sayısının sağına virgül eklenir. ( 1, )
- 10 sayısının da içinde 20 olmadığı için, 10'un sağına bir tane daha 0 eklenir.
- Kalan kısmında 100 sayısı olur.
- Bölüm kısmında bulunan 1, sayısının sağına sıfır eklenir. ( 1,0 )
- 100 sayısının içinde, 5 tane 20 vardır.
- 5 sayısı, bölüm kısmında olan 1,0 sayısının sağına yazılır.
- Bölüm kısmında 1,05 sayısı olur.
- Bölüm kısmına eklenen 5 sayısı ile bölen sayı çarpılır ( 5 . 20 = 100 )
- Bulunan sonuç, bölünmeye devam eden 100 sayısından çıkarılır. ( 100 - 100 = 0 )
- Kalan sayı sıfır (0) olduğu için işlem biter.
Kalan : 0
Bazı bölme işlemlerinde virgülden sonraki sonuç, aynı rakamların tekrarı (devri) şeklinde sonsuz rakamdan oluşur. Örneğin ( 20 / 6 ) işleminde sonuç 6,666.... şeklinde sonsuza uzanır. 6,666... sonucu, virgülden sonra devreden 6 rakamlarından ilkinin üst tarafına, çizgi konularak, 6,6 şeklinde yazılır. Devirli ondalık sonuçlu bölme işlemine, Sayılar 4. Bölüm » başlıklı yazıda değinilmiştir.
Bölme İşleminin Özellikleri
Bölme işleminin özellikleri:Yukarıdaki resimde belirtilen A, B, C ve K sayıları için:
A = B . C + K → Bölünen sayı, bölen sayı ile bölüm'ün çarpımının, kalan sayı ile toplanmasına eşittir.
Bölme işleminin özellikleri (A = B . C + K):
(23 / 5) işleminde:
Bölünen sayı (A) = 23
Bölen sayı (B) = 5
Bölüm (C) = 4
Kalan sayı (K) = 3'tür.
A = B . C + K
23 = 5 . 4 + 3 = 20 + 3 = 23
Bu örnekte, bölen sayı verilmemiş olsun. Verilmeyen bölen sayıya x diyelim.
23 = x . 4 + 3 → denklemi kurulur.
23 - 3 = 4x → (+3) sayısı, eşitliğin diğer tarafına geçtiğinde (-3) olur. (x . 4) ifadesi, 4x şeklinde yazılabilir.
20 = 4x → Eşitliğinde, eşitliğin her iki tarafı, 4 sayısına bölünür.
5 = x → 20 sayısı, 4'e bölündüğünde 5 olur. 4x ifadesi, 4'e bölündüğünde, 4 sayıları sadeleşir ve x yalnız kalır.
Bölen sayı verilmemiş olsa bile, verilen sayı değerleri, formülde yerine konularak, bölen sayı bulunabilir. Bölünen sayı, bölüm ve kalan sayı değerleri de formül aracılığı ile bulunabilir.
C < B → Bölme işleminde, bölen sayı, kalan sayıdan büyüktür. Bölme işlemi sonuçlandıysa, bölen sayı, kalan sayıdan büyük olmalıdır. Kalan bölümünde olan sayı, bölen sayıdan büyükse, bölme işlemi devam ediyor demektir.
K < C ise, B ile C yer değiştirebilir. Kalan sayı yine K olur → Bölme işleminde; bölüm (sonuç), kalan sayıdan büyük ise, bölüm ve bölen sayı yer değiştirebilir.
Bölme işleminin özellikleri (K < C ise, B ile C yer değiştirebilir. Kalan sayı yine K olur):
(23 / 5) işleminde:
Bölüm (C) = 4
Kalan sayı (K) = 3'tür ve bölüm, kalan sayıdan büyüktür. ( 3 < 4 )
Bu koşula göre, bölen sayı ve bölüm yer değiştirebilir. (23 / 5) işlemi için, bölen sayı ve bölüm yer değiştirirse, yapılan yeni işlem (23 / 4) işlemi olur.
(23 / 4) işleminde:
Bölüm (C) = 5
Kalan sayı (K) = yine 3'tür ve yine bölüm, kalan sayıdan büyüktür. (3 < 5)
5 . 4 + 3 = 4 . 5 + 3
Bölme işleminin özellikleri, (23 / 10) işlemi için:
(23 / 10) işleminde:
Bölüm (C) = 2
Kalan sayı (K) = 3'tür ve bu işlemde bölüm, kalan sayıdan küçüktür. ( 2 < 3 )
Bu koşula göre, bölen sayı ve bölüm yer değiştirse, kalan sayı, yapılan iki işlem için, birbirinden farklı olur.
(23 / 10) işlemi için, bölen sayı ve bölüm yer değiştirirse, yapılan yeni işlem (23 / 2) işlemi olur.
(23 / 2) işleminde:
Bölüm (C) = 11
Kalan sayı (K) = 1 olur.
10 . 2 + 3 = 2 . 11 + 1
K = 0 ise, A sayısı, B sayısına tam bölünür → Bölme işleminde, kalan sayı sıfır ise, bölünen sayı, bölen sayıya tam bölünür.
Not:
Bölme işleminde kalan sayı, bölen sayıdan küçüktür. ( K < B )
Kalan sayı sıfıra eşit veya sıfırdan büyük, bölen sayıdan küçüktür. ( 0 ≤ K < B )
Bölme işleminin özellikleri (K = 0 ise, A sayısı, B sayısına tam bölünür):
(30 / 6) işleminde:
Bölünen sayı (A) = 30
Bölen sayı (B) = 6
Bölüm (C) = 5
Kalan sayı (K) = 0 (Sıfırdır)
30 = 6 . 5 + 0 = 30 + 0 = 30
K = 0 ise
B sayısı, A sayısının tam bölenidir.
K = 0 ise, K < C 'dir ve bölüm ile bölünen sayı yer değiştirebilir.
B sayısı, A sayısının tam böleni ise, C sayısı da A sayısının tam bölenidir.
Örnek:
Bölme işlemi formül örnek soru (Kaynak: Supara):
Çözüm:
A = B . C + K formülünün açılımı:
Bölünen sayı = (Bölen sayı) . (Bölüm) + Kalan sayı
Bölme işlemi formül örnek soru çözümü:
Birinci bölme işlemi için:
a → Bölünen
b → bölen
2 → bölüm
3 → kalan ise,
a = b . 2 + 3 → (b . 2) ifadesi 2b şeklinde yazılırsa → a = 2b + 3
İkinci bölme işlemi için:
b → Bölünen
c → bölen
3 → bölüm
2 → kalan ise,
b = c . 3 + 2 → (c . 3) ifadesi 3c şeklinde yazılırsa → b = 3c + 2
a = 2b + 3 → ifadesinde b yerine, ikinci bölme işleminde bulunan b değeri olan (3c + 2) yazılır.
a = 2(3c + 2) + 3 → b yerine, ikinci bölme işleminde bulunan b değeri olan (3c + 2) yazıldığında oluşan yeni eşitlik
a = 2(3c + 2) + 3 işlemi için önce parantez açma işlemi yapılır.
2(3c + 2) parantezi, parantez dışında bulunan 2 sayısı ile açılır.
2 ile 3c çarpılır → 2 . 3c = 6c
2 ile 2 çarpılır → 2 . 2 = 4
Parentez içindeki (+) işareti, 6c ve 4 değerleri arasında bırakılır. → 6c + 4
Parantez işleminden sonra, 3 ile toplama işlemi yapılır. → 6c + 4 + 3 → 6c + 7
a = 6c + 7 olur.
Cevap: 6c + 7
Örnek:
Bölme işlemi örnek soru (kaynak: Supara)
Çözüm:
Bir bölme işleminde; kalan sayı (K), bölen sayıdan (B) küçük olmalıdır.
K < B
Bölünen sayı (A) tam bölünüyorsa; kalan sayı (K) sıfır olmalıdır.
Soruda verilen bölme işlemi için:
Bölen sayı (B) = 25
Bölüm (C) (Sonuç) = x + 4
Kalan sayı (K) = x²
Soruda, x sayısı tam sayı olarak tanımlanmıştır. Tam sayılar kümesi (-) negatif sayıları da içerir.
x² < 25 → K < B
x = (-4) için
x² = (-4) . (-4) = 16
Bölüm (C) = (x + 4) = (-4) + 4 = 0
x = (-3) için
x² = (-3) . (-3) = 9
Bölüm (C) = (x + 4) = (-3) + 4 = 1
x = (-2) için
x² = (-2) . (-2) = 4
Bölüm (C) = (x + 4) = (-2) + 4 = 2
x = (-1) için
x² = (-1) . (-1) = 1
Bölüm (C) = (x + 4) = (-1) + 4 = 3
x = 0 için
x² = 0 . 0 = 0
Bölüm (C) = (x + 4) = 0 + 4 = 4
x = 1 için
x² = 1 . 1 = 1
Bölüm (C) = (x + 4) = 1 + 4 = 5
x = 2 için
x² = 2 . 2 = 4
Bölüm (C) = (x + 4) = 2 + 4 = 6
x = 3 için
x² = 3 . 3 = 9
Bölüm (C) = (x + 4) = 3 + 4 = 7
x = 4 için
x² = 4 . 4 = 16
Bölüm (C) = (x + 4) = 4 + 4 = 8
x sayısının, (-4, -3, -2, -1, 0 , 1 , 2 , 3 ve 4) değerleri için x² < 25 koşulu sağlanır.
x = (-4) değeri için, bölüm (C) = 0 olur. (x + 4 = (-4) + 4 = 0)
Bir bölme işleminin sonucu sıfır (0) ise, bölünen sayı sıfır (0) olmalıdır. Sonuç sıfır (0) ise, kalan sayı da sıfır (0) olmalıdır.
x² = (-4) . (-4) = 16 kalan sayı değeri, sıfır (0) sonucu için mümkün olamaz.
Not:
Sıfır (0) sayısı, sıfır haricinde hangi sayıya bölünürse bölünsün, sonuç ve kalan sıfır (0) olur.
0 / 1 işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / (-5) işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / ∛5 işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / (-√3) işleminde, sonuç ve kalan sıfır (0) 'dır.
0 / 0 işlemi belirsiz bir işlemdir.
1 / 0 işlemi tanımsız bir işlemdir. (Sıfır hariç, tüm sayıların sıfıra (0) bölümü tanımsızdır.)
x = (-4) olamayacağı için, x sayısı 8 farklı değer alabilir. x sayısının 8 farklı değeri için, A sayısı da 8 farklı değer alır.
Cevap : 8
Aynı Sayıya Bölünen Farklı İki Sayının Kalan İlişkileri
x sayısının a ile bölümünden kalan my sayısının a ile bölümünden kalan n
olmak üzere:
(x ± y)'nin a ile bölümünden kalan (m ± n)'dir
Yukarıdaki ifade;
Birinci sayı olan x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
İkinci sayı olan y sayısının, yine a sayısına bölünmesi ile kalan sayının n olduğunu
Birinci sayı olan x ile ikinci sayı olan y'nin toplamının veya farkının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile y işleminin kalanı olan n'nin toplamı veya farkı olacağını ifade eder.
± → Sembolü ile verilen önermenin, hem toplama işlemi için hem çıkarma işlemi için geçerli olduğunu ifade edilir.
(x ± y)'nin a ile bölümünden kalan (m ± n)'dir:
Kalanların toplamı, bölen sayıdan küçükse:
Birinci sayı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İkinci sayı 34 olur ise, 34 sayısının, 8 sayısına bölümünden kalan, 2 olur.
Kurala göre, 41 ile 34'ün toplamının, 8 sayısına bölümünden kalan ( 2 + 1 = 3) olmalıdır.
Kalan sayıların toplamı olan 3, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 + 34 = 75
75 sayısının 8 ile bölümünden kalan 3 olur.
Kalanların toplamı, bölen sayıdan büyükse:
Birinci sayı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
İkinci sayı 52 olur ise, 52 sayısının, 8 sayısına bölümünden kalan, 4 olur.
Kurala göre, 47 ile 52'in toplamının, 8 sayısına bölümünden kalan ( 7 + 4 = 11) olmalıdır.
Kalan sayıların toplamı olan 11, bölen sayı olan 8'den büyük olduğu için 11 sayısı, tekrar 8 sayısına bölünür.
11 sayısının, 8 sayısına bölümünden kalan, 3 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 + 52 = 99
99 sayısının 8 ile bölümünden kalan 3 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 2 ise
(a - b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4'ten, b sayısının 5 ile bölümünden kalan sayı olan 2 çıkarılırsa, (a - b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 - 2 = 2
Bulunan 2 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 3 ise
(a + b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4 ile b sayısının 5 ile bölümünden kalan sayı olan 3 toplanırsa, (a + b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 + 3 = 7
Kalan sayıların toplamı olan 7, bölen sayı olan 5 sayısından büyük olduğundan; 7 sayısı, 5 sayısına bölünür.
7 sayısının, 5 sayısına bölümünden kalan, 2 olur.
Cevap : 2
(x . y)'nin a ile bölümünden kalan (m . n)'dir
Yukarıdaki ifade;
Birinci sayı olan x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
İkinci sayı olan y sayısının, yine a sayısına bölünmesi ile kalan sayının n olduğunu
Birinci sayı olan x ile ikinci sayı olan y'nin çarpımının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile y işleminin kalanı olan n'nin çarpımı olacağını ifade eder.
(x . y)'nin a ile bölümünden kalan (m . n)'dir:
Kalanların çarpımı, bölen sayıdan küçükse:
Birinci sayı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İkinci sayı 34 olur ise, 34 sayısının, 8 sayısına bölümünden kalan, 2 olur.
Kurala göre, 41 ile 34'ün çarpımının, 8 sayısına bölümünden kalan ( 2 . 1 = 2) olmalıdır.
Kalan sayıların çarpımı olan 2, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 . 34 = 1394
1394 sayısının 8 ile bölümünden kalan 2 olur.
Kalanların çarpımı, bölen sayıdan büyükse:
Birinci sayı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
İkinci sayı 52 olur ise, 52 sayısının, 8 sayısına bölümünden kalan, 4 olur.
Kurala göre, 47 ile 52'in çarpımının, 8 sayısına bölümünden kalan ( 7 . 4 = 28) olmalıdır.
Kalan sayıların çarpımı olan 28, bölen sayı olan 8'den büyük olduğu için 28 sayısı, tekrar 8 sayısına bölünür.
28 sayısının, 8 sayısına bölümünden kalan, 4 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 . 52 = 2444
2444 sayısının 8 ile bölümünden kalan 4 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 1
b sayısının 5 ile bölümünden kalan 2 ise
(a . b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 1 ile, b sayısının 5 ile bölümünden kalan sayı olan 2 çarpılırsa, (a . b) sayısının 5 ile bölümünden kalan sayı bulunur.
1 . 2 = 2
Bulunan 2 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4
b sayısının 5 ile bölümünden kalan 3 ise
(a . b) sayısının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı olan 4 ile, b sayısının 5 ile bölümünden kalan sayı olan 3 çarpılırsa, (a . b) sayısının 5 ile bölümünden kalan sayı bulunur.
4 . 3 = 12
Kalan sayıların çarpımı olan 12, bölen sayı olan 5 sayısından büyük olduğundan; 12 sayısı, 5 sayısına bölünür.
12 sayısının, 5 sayısına bölümünden kalan, 2 olur.
Cevap : 2
(t . x)'nin a ile bölümünden kalan (t . m)'dir
Yukarıdaki ifade;
x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
x sayısı ile t sayının çarpımının, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m ile t sayısının çarpımı olacağını ifade eder.
(t . x)'nin a ile bölümünden kalan (t . m)'dir:
t sayısı ile kalan sayının çarpımı, bölen sayıdan küçükse:
x sayısı 41 olur ise, 41 sayısının, 8 sayısına bölümünden kalan, 1 olur.
t sayısı 3 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre, 41 ile t sayısı olan 3'ün çarpımının, 8 sayısına bölümünden kalan ( 1 . 3 = 3) olmalıdır.
Kalan sayı ile t sayısının çarpımı olan 3, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
41 . 3 = 123
123 sayısının 8 ile bölümünden kalan 3 olur.
t sayısı ile kalan sayının çarpımı, bölen sayıdan büyükse:
x sayısı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre, 47 ile t sayısı olan 2'nin çarpımının, 8 sayısına bölümünden kalan ( 7 . 2 = 14) olmalıdır.
Kalan sayı ile t sayısının çarpımı olan 14, bölen sayı olan 8'den büyük olduğu için 14 sayısı, tekrar 8 sayısına bölünür.
14 sayısının, 8 sayısına bölümünden kalan, 6 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47 . 2 = 94
94 sayısının 8 ile bölümünden kalan 6 olur.
Örnek:
a sayısının, 5 ile bölümünden kalan 1'dir.
a sayısının 4 katının, 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı 1 ise,
a sayısının dört katının 5 ile bölümünden kalan sayı,
a sayısının 5 ile bölümünden kalan sayı olan 1'in dört katıdır.
1 . 4 = 4
Bulunan 4 sayısı, bölen sayı olan 5'ten küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 5 ile bölümünden kalan 4'dür.
a sayısının 102 katının 5 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 5 ile bölümünden kalan sayı 4 ise,
a sayısının 102 katının 5 ile bölümünden kalan sayı,
a sayısının 5 ile bölümünden kalan sayı olan 4'ün 102 katıdır.
4 . 102 = 408
Kalan sayı ile t sayısının çarpımı olan 408, bölen sayı olan 5 sayısından büyük olduğundan; 408 sayısı, 5 sayısına bölünür.
408 sayısının, 5 sayısına bölümünden kalan, 3 olur.
Cevap : 3
x'in t'ninci kuvvetinin a ile bölümünden kalan, m'nin t'ninci kuvvetidir
Yukarıdaki ifade;
x sayısının, a sayısına bölünmesi ile kalan sayının m olduğunu
x sayısının t'ninci kuvvetinin, yine a sayısına bölünmesi ile kalan sayının, x işleminin kalanı olan m sayısının, t'ninci kuvveti olduğunu ifade eder.
x'in t'ninci kuvvetinin a ile bölümünden kalan, m'nin t'ninci kuvvetidir:
Kalan sayının t'ninci kuvveti, bölen sayıdan küçükse:
x sayısı 42 olur ise, 42 sayısının, 8 sayısına bölümünden kalan, 2 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre:
42 sayısının, 8 sayısına bölümünden kalan sayı olan 2'nin 2. kuvveti (2²),
42 sayısının 2. kuvvetinin (42²), 8 sayısına bölümünden kalan sayıdır. (2² = 2 . 2 = 4 )
Kalan sayının 2. kuvveti olan 4, bölen sayı olan 8'den küçüktür.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
42² = 42 . 42 = 1764
1764 sayısının 8 ile bölümünden kalan 4 olur.
Kalan sayının t'ninci kuvveti, bölen sayıdan büyükse:
x sayısı 47 olur ise, 47 sayısının, 8 sayısına bölümünden kalan, 7 olur.
t sayısı 2 olsun diyelim. (Herhangi bir pozitif tam sayı olabilir.)
Kurala göre:
47 sayısının, 8 sayısına bölümünden kalan sayı olan 7'nin 2. kuvveti (7²),
47 sayısının 2. kuvvetinin (47²), 8 sayısına bölümünden kalan sayıdır. (7² = 7 . 7 = 49 )
Kalan sayının 2. kuvveti olan 49, bölen sayı olan 8'den büyük olduğu için 49 sayısı, tekrar 8 sayısına bölünür.
49 sayısının, 8 sayısına bölümünden kalan, 1 olur.
İşlem yapılmadan da bulunabilen kalan sayı, işlem yapıldığında da aynı çıkmalıdır.
47² = 47 . 47 = 2209
2209 sayısının 8 ile bölümünden kalan 1 olur.
Örnek:
a sayısının, 9 ile bölümünden kalan 2 ise
a³ sayısının, 9 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 9 ile bölümünden kalan sayı 2 ise,
a sayısının 3.kuvvetinin 9 ile bölümünden kalan sayı,
a sayısının 9 ile bölümünden kalan sayı olan 2'nin 3.kuvvetidir.
2³ = 2 . 2 . 2 = 8
Bulunan 8 sayısı, bölen sayı olan 9'dan küçük olduğundan, başka bir işlem yapılmaz.
Örnek:
a sayısının, 9 ile bölümünden kalan 2 ise
a⁵ sayısının, 9 ile bölümünden kalan kaçtır?
Çözüm:
a sayısının 9 ile bölümünden kalan sayı 2 ise,
a sayısının 5.kuvvetinin 9 ile bölümünden kalan sayı,
a sayısının 9 ile bölümünden kalan sayı olan 2'nin 5.kuvvetidir.
2⁵ = 2 . 2 . 2 . 2 . 2 = 32
Kalan sayının 5. kuvveti olan 32, bölen sayı olan 9 sayısından büyük olduğundan; 32 sayısı, 9 sayısına bölünür.
32 sayısının, 9 sayısına bölümünden kalan, 5 olur.
Cevap : 5
Örnek:
x ve y pozitif tam sayılardır.
x in 6 ile bölümünden kalan 2,
y nin 6 ile bölümünden kalan 5 olduğuna göre
x.y + y² nin 6 ile bölümünden kalan kaçtır? (Kaynak: Supara)
Çözüm:
Aynı sayıya bölünen sayıların kalan ilişkilerinde, toplama ve çarpma işlemi (veya diğer işlemler) birlikte kullanılıyorsa, işlemler kalan sayılar ile yapılır.
x in 6 ile bölümünden kalan 2 ise (x.y + y²) işleminde, x yerine 2 yazılır. (x = 2)
y nin 6 ile bölümünden kalan 5 ise (x.y + y²) işleminde, y yerine 5 yazılır. (y = 5)
x = 2
y = 5 için
x.y + y² = 2 . 5 + 5² = 10 + 25 = 35
Çıkan sonuç 6 sayısından küçük olsaydı, bulunan sonuç, (x.y + y²) işleminin, 6 ile bölümünden kalan olacaktı.
Çıkan sonuç olan 35 sayısı, 6 sayısından büyük olduğundan, (x.y + y²) işleminin, 6 ile bölümünden kalan:
35 sayısının 6 ile bölümünden kalandır. 35 sayısı, 6 ile bölündüğünde kalan sayı 5 olur.
Cevap: 5



















Yorumlar
Yorum Gönder